Tecnofilosofia: come le moderne tecnologie informatiche sono emerse dalla filosofia

L'informatica ha una storia particolare, in questa storia la filosofia gioca un ruolo essenziale, il problema è che su questo ruolo la maggior parte tacciono.
Io qui ho intenzione di parlare proprio di questo:
di come l'ultima rivoluzione tecnologica sia emersa dalla filosofia e come le idee dei filosofi siano confluite in essa.
La tecnofilosofia è una specie di settore scientifico all'interno della filosofia di mia invenzione.
In questo testo e in altri parlerò di questa disciplina e nel particolare cercherò di rintracciarne le origini e le basi nella filosofia.
La tecnofilosofia nello specifico intende essere la scienza delle tecnologie basate sulla logica.
Questa definizione, tuttavia, spero che negli anni venga estesa ed arricchita.
Quello che ho in mente di fare con la tecnofilosofia, così come con altre materie come la matematica filosofica, di cui in parte ho già parlato, consiste nel superare quel vecchio approccio della filosofia sulle scienze nel quale la filosofia prende la scienza come oggetto, ma si rivolge a questa sempre come a qualcosa di esterno e di diverso.
Quando troviamo dei settori della filosofia denominati "filosofia della...", che sia filosofia della fisica, della biologia, della neuroscienze, sono tutti ambiti che partono dall'epistemologia intesa come filosofia della scienza.
Ognuno di questi ambiti tratta la scienza come qualcosa di esterno e come oggetto di studio.
Il filosofo della scienza studia la fisica, senza fare fisica. Egli studia piuttosto le condizioni di possibilità della fisica: i suoi fondamenti.
Un ambito più interessante è oggi quello dell'ontologia, in quanto l'ontologia si interessa di tutto ciò che esiste di ciò che c'è e dell'essere di ciò che esiste.
È possibile un'ontologia di ogni cosa:
della mente, della biologia, delle neuroscienze, della fisica, della chimica, della società, ecc.
Gli studi dell'ontologia sono molto interessanti, in quanto mostrano una filosofia che vorrebbe fare scienza sperimentale.
Per esempio in bioontologia esiste questo dibattito tra chi crede che le specie siano essenze segnate da un codice di DNA fisso e chi crede che le specie siano la semplice produzione contingente di un processo evolutivo che continua.
Dico che è interessante perché si potrebbero studiare queste posizioni con ricerche sperimentali, perché queste ricerche potrebbero spiegarci quale delle due posizioni è più corretta.
La tecnofilosofia ha per oggetto la tecnologia ed in particolare la tecnologia informatica.
La tecnofilosofia deve trarre vantaggio dal sapere proveniente dalla filosofia dell'informatica, ma non svolge lo stesso ruolo.
La filosofia dell'informatica non è un ambito molto sviluppato nella filosofia. Tuttavia essa annovera già qualche nome noto.
In filosofia analitica i principali filosofi dell'informatica sono Luciano Floridi, Hubert Dreyfus e Barry Smith.
Luciano Floridi è un famoso filosofo dell'informatica italiano che insegna ad Oxford. Egli è il padre della prima etica dell'informatica e di una teoria dell'informazione.
Dreyfus è noto nell'ambito della filosofia informatica principalmente per due opere: On internet; What computers still can not do.
Dreyfus è uno studioso dell'intelligenza artificiale, ma anche un suo critico. I suoi testi hanno principalmente lo scopo di mostrare la sostanziale differenza tra l'intelligenza del computer e quella umana.
Barry Smith si è interessato principalmente di ontologia informatica e il problema dei data base.
L'ontologia informatica è un ambito molto interessante perché non è solamente filosofico, ma anche informatico.
È la prova che gli informatici si stanno interessando di filosofia e i filosofi farebbero meglio ad interessarsi di informatica.
L'ontologia informatica, detto con parole semplici, riprende il concetto di ontologia classico come classificazione di ciò che esiste, esemplificato nella dialettica di Aristotele, applicandolo all'informatica, in particolare ai data base.
Recentemente si nota anche una filosofia dell'informatica nella filosofia continentale. I principali autori qui sono Manuel De Landa e Aden Evens.
Manuel De Landa pare sia particolarmente interessato alla programmazione e ha scritto dei testi come La guerra nell'era delle macchine intelligenti, dove cerca di mostrare un lato deleuziano dell'informatica.
Aden Evens, dal mio punto di vista, si avvina molto al primo tecnofilosofo. Evens ha scritto un libro (Logic of the digital) dove illustra come funziona il computer partendo dai bit, passando per gli oggetti e le interfacce, fino ad arrivare al web.
Per parlare del modo in cui l'informatica è emersa a patire dalla filosofia esistono due vie interessanti:
la prima parte dall'importante contributo della logica filosofica nell'informatica;
la seconda parte da quelle tecnologie, vecchi calcolatori, rispetto ai quali certamente si può pensare che il computer sia stata un'evoluzione.
Preferirei partire da questo ultimo elemento perché lo trovo davvero importante per la tecnofilosofia.
Se la tecnofilosofia mira non semplicemente allo studio di tecnologie, ma anche alla costruzione di esse, allora è legittimo chiedersi per quale motivo io reputo che un filosofo potrebbe costruire tecnologie.
La risposta è perché lo ha già fatto.
Studiando la storia della filosofia mi sono accorto che sono esistiti per davvero dei filosofi che hanno costruito delle tecnologie.
Ho in mente principalmente due filosofi: Blaise Pascal e Gottfiried Wilhem Leibniz.
Pascal ha creato la "pascaliana" e Leibniz "la macchina di Leibniz". Entrambi sono dei calcolatori, o meglio delle calcolatrici.
Certamente Leibniz e Pascal erano anche dei matematici.
All'epoca la filosofia non era completamente distinta dalle altre scienze e nemmeno dall'ambito tecnologico, a quanto pare.
La filosofia con Kant e dopo di Kant, ossia la filosofia che si pensa come scienza essa stessa, separata dalle altre scienze, conosce una separazione. Tuttavia, perché no?
perché non dovrebbe essere ancora possibile ricongiungere quel filo che connetteva la filosofia con la tecnologia?
Vediamo più da vicino questi due calcolatori.
Cominciamo pure dalla pascaliana.

Il calcolatore di Pascal è una macchina che permette di eseguire operazioni matematiche di calcolo come la somma e la sottrazione. È stata pensata da Pascal per alleggerire e facilitare il lavoro del padre.
Pascal dedicò poi questa macchina a Pierre Séguier, cancelliere della Francia, il quale gli diede i diritti esclusivi per la costruzione di tale calcolatore.
Leibniz penserà la sua macchina ispirandosi proprio al lavoro di Pascal. Si noti, cosa sorprendente, che Pascal stava lavorando alla sua macchina già all'età di venti anni.
Il calcolatore di Pascal ha dei quadranti circolari con ruote a raggi con delle cifre che vanno da 0 a 9.
Esattamente come nei vecchi telefoni di casa, dove bisognava girare il dito fino ad un punto dove si trova un fermo per digitare un numero da chiamare, in modo simile i raggi della ruota del quadrante devono girare fino ad un punto.
L'input viene da questa rotazione e questa produce un risultato numerico che appare in alto nella macchina in una finestra di visualizzazione. Per ruotare i raggi è sufficiente un semplice stilo.
Grazie a queste rotazioni è possibile compiere delle somme tra numeri.
Se voglio una cifra che abbia più di un numero, allora devo usare più quadranti.
Se, per esempio, la cifra contenesse due numeri, allora basterebbe ruotare un quadrate per un numero e l'altro per l'altro numero.
Poniamo che il numero sia 34, ne segue che il primo quadrante deve segnare 4 e il secondo 3.
Se intendo sommare a 34 29 devo aggiungere 2 al secondo quadrante e 9 al primo.
Dunque prima ruoto il secondo quadrante fino ad arrivare al numero 5, poi ruoto il primo quadrante fino arrivare al numero 3.
A questo punto nel secondo quadrante il numero segnato non sarà più 5, ma sarà 6.
Il risultato della somma è dato nelle prime due finestre di visualizzazione ed è 63.
Ci sono 5 quadranti e ogni volta che un quadrante viene girato fino al numero 9, il quadrante successivo aggiunge uno. Quando si arriva a 99999 aggiungendo 1 il numero finale sarà 00000.
È possibile anche compiere una sottrazione, ma il meccanismo è più complesso: bisogna usare il complemento di 9.
Nel calcolatore di Pascal troviamo anche una barra sopra che può essere spostata sotto, di modo da far comparire altre finestre di visualizzazione che non apparivano prima.
Nella seconda serie delle finestre, prima coperte, stanno i complementi di 9. Per sottrarre due numeri il procedimento non è molto diverso da come si faceva prima: si tratta sempre ruotare i quadranti sotto della quantità che si intende sottrarre. Ovviamente per moltiplicare basta sommare n volte un certo numero, ossia 4 x 4 = 4 + 4 + 4 + 4.
Come funziona all'interno il calcolatore di Pascal?
Ogni quadrante con la sua ruota a raggi, facendo ruotare la ruota, fa ruotare altri ingranaggi interni: una ruota più grande dentellata che fa ruotare un'altra ruota che compone un accumulatore.
L'ingranaggio fa poi ruotare una piccola ruota generando il movimento dei numeri nella finestra di visualizzazione. Esistono due perni nell'accumulatore che fanno sì che un meccanismo si attivi quando arriva al numero 9 per dare un comando all'accumulatore del quadrante di fianco.
La macchina di Leibniz è ispirata a quella di Pascal, ma allo stesso tempo è diversa.

La macchina di Leibniz è nota anche come Stepped Reckoner, costruita in ottone lucido ed acciaio.
La macchina è composta da due parti principali: un accumulatore dietro e le classiche finestre di visualizzazione dei risultati, che questa volta sono sedici; una parte davanti per dare l'input, ossia una manopola che permette di selezionare un numero da 0 a 9.
Le manopole in totale sono 8. Una volta selezionato il numero si gira una manovella per eseguire l'operazione aritmetica.
Se selezioniamo 0, girando la manovella non otterremo assolutamente nulla, perché il meccanismo è fatto in modo che sullo zero non aggiunga nulla. Un numero qualsiasi più zero è uguale a se stesso.
Se selezionassimo 3, girando la manovella vedremo 3 nella nostra finestra di visualizzazione. Se poi selezionassimo 5, potremmo aggiungere questa quantità ruotando la manovella ancora una volta e otteniamo 8 come risultato.
Per sottrarre si ruota la manovella al contrario, mentre per moltiplicare bisogna sommare un certo numero di volte o sottrarre, se si intende dividere.
Il segreto della Stepped Reckoner sta nella sua ruota, una ruota legata alla manovella, la quale, una volta che viene digitato un numero diverso da zero, fa girare una ruota dentellata che fa ruotare i numeri nella finestra di visualizzazione.
Queste macchine erano a quei tempi delle grandi innovazioni. Viste oggi ci possono sembrare degli antenati dei moderni calcolatori, ma si potrebbero considerare anche degli antenati del computer, sotto certi aspetti.
Oggi, tuttavia, grazie alla programmazione, costruire un calcolatore è un gioco da ragazzi.
Per esempio, usando due linguaggi come Html e Php, potrete facilmente creare un calcolatore che è in grado di sommare, sottrarre, moltiplicare e dividere.
Scrivete in un foglio html un testo di questo tipo:
<form>
<input type="text" name="num1" placeholder="numero 1" />
<input type="text" name="num2" placeholder="numero 2" />
<select name="operator">
<option>Nessuno</option>
<option>Addizione</option>
<option>Sottrazione</option>
<option>Moltiplicazione</option>
<option>Divisione</option>
</select>
<br/>
<button name="submit" value="submit" type="submit">Calcolare</button>
</form>
<p>La risposta è: </p>
Con questo testo noi stiamo impostando le basi per il calcolo.
Abbiamo due caselle di testo ("text") dove mettere i due numeri, c'è un selettore ("select") che ci permette di scegliere tra l'addizione, la sottrazione, la moltiplicazione e la divisione, c'è un pulsante ("submit") che ci permette di inviare i nostri input.
Tuttavia, perché il calcolatore funzioni e scriva come output, accanto alla frase "La risposta è:", il suo risultato, dovrete scrivere ancora questo codice in Php:
<?php
if(isset($_GET['submit'])) {
$risultato1 = $_GET['num1'];
$risultato2 = $_GET['num2'];
$operator = $_GET['operator'];
switch($operator) {
case 'None':
echo "You need to select a method";
break;
case 'Addizione':
echo $risultato1 + $risultato2;
break;
case 'Sottrazione':
echo $risultato1 - $risultato2;
break;
case 'Moltiplicazione':
echo $risultato1 * $risultato2;
break;
case 'Divisione':
echo $risultato1 / $risultato2;
break;
}
}
Sfruttando le variabili e uno switch, questo codice ci permette di, una volta selezionata l'operazione che vogliamo compiere, eseguire quell'operazione di calcolo con i numeri inseriti nelle caselle di testo.
Quella dei calcolatori è solo una parte della storia, se si vogliono comprendere le origini dell'informatica.
Per conoscere l'altra parte bisogna rivolgersi alla storia della logica e incominciare da lontano: da Aristotele.
L'Organon è l'opera nella quale Aristotele definisce i fondamenti della logica classica. Lui stesso è il padre della logica classica, una logica che non era ancora matematizzata.
Questa logica viene fondata da Aristotele su tre principi fondamentali:
1) Principio di identità: ogni cosa è identica a se stessa.
2) Principio di terzo escluso: o una cosa ha una certa proprietà o non la possiede affatto.
3) Principio di non contraddizione: è impossibile che una cosa abbia e non abbia una certa proprietà.
Tutte le logiche alternative alla classica sono logiche che negano almeno uno di questi principi, se non completamente, almeno per un certo numero di casi.
Questi principi sono le basi della logica classica, ma Aristotele ha scoperto anche dell'altro: i quantificatori.
Un quantificatore è un'espressione come "tutti o nessuno" oppure "alcuni".
"Tutti" è un quantificatore universale, mentre "alcuni" è un quantificatore esistenziale. A partire da questi concetti Aristotele pensa il sillogismo come metodo deduttivo che permette di passare dal generale al particolare. Un esempio:
1 Tutti i gatti sono felini.
2 Felix è un gatto.
3 Felix è un felino.
1 e 2 sono delle premesse, mentre 3 è la conclusione.
Nella premessa 1 compare il quantificatore universale "Tutti", la seconda premessa e la conclusione rappresentano un caso particolare.
La prima premessa afferma che ogni gatto ha la proprietà di essere un felino.
La seconda premessa ci dice che Felix, come individuo, è un gatto.
Dunque possiamo concludere se Felix è un gatto e tutti i gatti sono felini, allora anche Felix deve essere un felino.
"Essere gatto" qui funge da termine medio nel sillogismo e permette di dedurre la conclusione. Tutti questi enunciati sono del tipo soggetto/predicato.
Il termine medio è nella prima premessa un soggetto e nella seconda un predicato. Gli altri due termini compaiono nella loro posizione alla conclusione.
Dopo Aristotele vengono gli stoici. Gli stoici vanno almeno ricordati per la scoperta dei connettivi e l'invenzione della logica enunciativa.
I connettivi che si devono agli stoici sono almeno tre:

La logica sarà finalmente matematizzata nell'800' con George Boole, ma cos'è Boole se non un grande lettore di Aristotele? Boole è importante in questa storia per molti motivi, principalmente per la matematizzazione della logica di Aristotele e quella degli stoici.
È stato il primo a cercare di tradurre quelle due logiche che sembravano così diverse in un unico linguaggio.
Principalmente le scoperte di Boole sono tre:
l'attribuzione ai numeri 1 e 0 del significato di vero e di falso;
la matematizzazione del principio di non contraddizione;
la scoperta degli operatori and, or e not.
Boole arriva a pensare che vero = 1 e falso = 0. La logica di Boole è basata principalmente su questi due numeri e questi numeri sono i fondamenti di tutta l'informatica perché costituiscono il codice binario.
In logica il discorso è il seguente: se prendo l'enunciato "Mio zio si chiama Sam", se è vero, ossia se mio zio si chiama davvero Sam, allora posto che x = "Mio zio si chiama Sam", ne consegue che x = 1.
Nel caso in cui questo enunciato sia falso, ne segue che x = 0. La logica di Boole segue la regola "o tutto o niente". Boole scopre l'abisso di Leibniz, quell'abisso che separa il nulla da qualcosa.
La domanda di Leibniz era: perché l'essere piuttosto che il nulla? In Boole questa domanda potrebbe diventare: perché 1 piuttosto che 0?
In fondo quando parliamo di 1 e 0, parliamo sempre del grande vecchio dualismo, come quello tra il bene e il male, il brutto e il bello, ecc. 0, tuttavia, è niente, mentre 1 è tutto.
Il fatto sopra citato lo si constata molto bene se si analizza la formula fondamentale di Boole: quella del principio di non contraddizione.
Aristotele la considerava come uno dei principi più importanti della logica classica ed è quello che regge la maggior parte dei suoi discorsi nella Metafisica.
Il metodo della divisione nell'ontologia, ad esempio, suppone che un modello ontologico non possieda dei rombi.
Se sto facendo un'ontologia delle automobili, non posso dividere prima le automobili per marca (Mercedes, Bmw, Audi, Cytroen, Fiat, ecc..) e poi per colore (grigio, verde, rosso, ecc.) perché in quel caso avrei macchine Bmw grige e Mercedes grigie, ossia otterrei una classe di macchine grigie che sono sia Bmw che Mercedes.
Il principio di non contraddizione è posto proprio per evitare questi casi. Boole pensa il principio di non contraddizione come elemento fondamentale della sua teoria e lo esprime con questa formula:
x(1-x) = 0
Se x = tucano e 1 - x = tutti gli uccelli che non sono tucani, allora possiamo pensare che l'affermazione secondo la quale "Tutti gli uccelli tranne i tucani sono tucani" è contraddittoria, ossia falsa (= 0).
Nella formula della non contraddizione incontriamo un operatore booleano che è il not.
Il not funziona in questo modo:
1 - x
1 - 1 = 0
1 - 0 = 1
Se x è vero, allora 1 - x è falso. Se x è falso, allora 1 - x è vero. Oltre al not Boole scopre anche l'or e l'and, i quali corrispondo in logica alla disgiunzione e alla congiunzione.
L'or segue questa regola:
x + y
1 + 1 = 1
0 + 1 = 1
1 + 0 = 1
0 + 0 = 0
(1 + 1 = 1, semplicemente perché non c'è numero più grande di 1 nella logica booleana.)
L'and segue quest'altra regola:
x * y
1 * 1 = 1
0 * 1 = 0
1 * 0 = 0
0 * 0 = 0
Ogni volta, a seconda che x o y siano vere o false, cambia il risultato dell'operazione.
L'elemento essenziale per quanto riguarda and, or e not, sta nel fatto che questi operatori sono la traduzione matematica dei connettivi della logica enunciativa degli stoici.
Dopo Boole si è sviluppata quella che propriamente definiamo oggi come "algebra booleana".
Una delle parti più importanti di questa disciplina è costituita dai circuiti booleani. Essa costituisce una parte essenziale in questa storia che vi sto raccontando, in quanto permette di comprendere il ruolo successivo dell'elettronica nell'informatica, in particolare l'unione della logica con l'elettronica.
I circuiti booleani sono composti dagli operatori di Boole, più altri operatori che derivano da questi.
Il primo operatore da vedere è il not.
Esso ha una sola entrata e una uscita. In questo caso l'1 e lo 0 stanno per l'aperto e il chiuso. 1 è aperto e 0 è chiuso.
Operatore Not:
Se ingresso = 1, allora l'uscita sarà = 0
Se ingresso = 0, allora l'uscita sarà = 1
Gli operatori and e or, invece hanno due ingressi e una sola uscita.
Operatore And:
Se ingresso A = 0 e ingresso B = 0, allora l'uscita sarà = 0
Se ingresso A = 1 e ingresso B = 0, allora l'uscita sarà = 0
Se ingresso A = 0 e ingresso B = 1, allora l'uscita sarà = 0
Se ingresso A = 1 e ingresso B = 1, allora l'uscita sarà = 1
Operatore Or:
Se ingresso A = 0 e ingresso B = 0, allora l'uscita sarà = 0
Se ingresso A = 1 e ingresso B = 0, allora l'uscita sarà = 1
Se ingresso A = 0 e ingresso B = 1, allora l'uscita sarà = 1
Se ingresso A = 1 e ingresso B = 1, allora l'uscita sarà = 1
Se conoscete le tavole della verità della congiunzione e della disgiunzione in logica vi renderete conto che i risultati sono gli stessi.
Tuttavia vi basta semplicemente confrontare quello che ho scritto qui con quello che scritto prima su and e or in Boole.
Esistono altri operatori che si compongono di and, or e not.
In particolare questi operatori sono tre: nand, nor e xor.
Operatore Nand (not + and):
Se ingresso A = 0 e ingresso B = 0, allora l'uscita sarà = 1
Se ingresso A = 1 e ingresso B = 0, allora l'uscita sarà = 1
Se ingresso A = 0 e ingresso B = 1, allora l'uscita sarà = 1
Se ingresso A = 1 e ingresso B = 1, allora l'uscita sarà = 0
Operatore Nor (not + or):
Se ingresso A = 0 e ingresso B = 0, allora l'uscita sarà = 1
Se ingresso A = 1 e ingresso B = 0, allora l'uscita sarà = 0
Se ingresso A = 0 e ingresso B = 1, allora l'uscita sarà = 0
Se ingresso A = 1 e ingresso B = 1, allora l'uscita sarà = 0
Operatore xOr:
Se ingresso A = 0 e ingresso B = 0, allora l'uscita sarà = 0
Se ingresso A = 1 e ingresso B = 0, allora l'uscita sarà = 1
Se ingresso A = 0 e ingresso B = 1, allora l'uscita sarà = 1
Se ingresso A = 1 e ingresso B = 1, allora l'uscita sarà = 0
Quel che è importante capire è che partendo da un operatore si può collegare un altro, collegando l'uscita del primo con l'ingresso del secondo. Con questo metodo possiamo costruire circuiti booleani sempre più complessi.
Una volta compreso il modo in cui è possibile tradurre la logica booleana nell'elettronica possiamo capire il lavoro di uno dei due padri dell'informatica: Claude Shannon.
Claude Shannon era affascinato da George Boole ed è lui che per primo applicò l'algebra booleana ai circuiti elettronici.
Shannon è famoso per la suo scritto: A symbolic analisis of relay and switching circuits.
Per capire il lavoro di Shannon ci serve un po' di terminologia o definizioni. Chiamiamo i terminali con le lettere minuscole a, b, c, d, e, ecc. I circuiti che mettono assieme i terminali sono chiamati con le lettere maiuscole X, Y, Z, W, ecc. Quando un circuito è aperto, ossia quando passa la corrente, il circuito è 1. Quando un circuito è chiuso, ossia quando non passa la corrente, il circuito è 0. Dunque il circuito Y(ab) se è = 1, allora è aperto, se è = 0, allora chiuso. Questi circuiti, inoltre, possono essere addizionati o moltiplicati. Qui entrano in gioco due operatori di Boole: and e or.
Se metto i due circuiti con i relativi terminali in serie, è come se moltiplicassi i due circuiti (X*Y). Posso farlo in questi modi differenti, a seconda che i circuiti siano 1 o 0:
se X = 0 e Y = 0, allora 0 * 0 = 0
se X = 1 e Y = 0, allora 1 * 0 = 1
se X = 0 e Y = 1, allora 0 * 1 = 1
se X = 1 e Y = 1, allora 1 * 1 = 1
Se metto i due circuiti in parallelo, è come se sommassi i due circuiti (X + Y). Posso farlo nei seguenti modi, a seconda che i circuiti siano 1 o 0:
se X = 0 e Y = 0, allora 0 + 0 = 0
se X = 1 e Y = 0, allora 1 + 0 = 0
se X = 0 e Y = 1, allora 0 + 1 = 0
se X = 1 e Y = 1, allora 1 + 1 = 1
Con questi elementi di base è possibile costruire un circuito complesso in serie-parallelo.
Prendiamo la seguente equazione ad esempio:
W = A + B + (C · W)
Vediamo chiaramente che A, B e (C · W) sono in parallelo, ma C e W sono in serie tra di loro. Lo vediamo perché prima abbiamo delle somme, dunque degli elementi in parallelo.
Successivamente vediamo due elementi moltiplicati, dunque in serie. Ma i circuiti in serie costituiscono un or e quelli in parallelo un and. Sono questi gli elementi principali che mettono in evidenza l'utilizzo da parte di Claude Shannon dell'algebra booleana.
Ricapitolando, si parte dalla logica degli stoici e di Aristotele per passare per Boole e infine arrivare all'elettronica di Shannon.
Dalla filosofia all'elettronica, passando per la matematica.

Per capire l'ultimo passaggio, ossia per arrivare al famoso Alan Turing, conviene prima tornare alla filosofia, precisamente a Frege e ai fondamenti della logica predicativa.
Con Frege nasce un modo di fare logica in senso matematico differente rispetto al modello di Boole. Frege è considerato il padre della logica predicativa. Qui non ci serve conoscere nel dettaglio la teoria di Frege, ci bastano alcune basi di logica predicativa.
La logica predicativa, a differenza di quella enunciativa, riesce ad analizzare la struttura interna di un enunciato.
Frege ha avuto questa brillante intuizione:
intendere l'enunciato soggetto/predicato e l'enunciato di relazione come delle funzioni matematiche.
Se prendiamo l'addizione come una funzione (A) che ha come argomento dei numeri (es. 1, 2), allora possiamo scrivere: A(1,2) = 3. Stiamo semplicemente sommando i due numeri.
Possiamo fare la stessa cosa con il successore e scrivere: S(4) = 5. Il numero successivo a 4 è, infatti, 5. Se prendo un enunciato semplice come "Paperino è un'anatra", posso scrivere questo enunciato considerando "anatra" come funzione e "Paperino" come suo argomento. In questo senso scriverò qualcosa di simile: Ap. La lettera maiuscola si definisce come lettera predicativa e la lettera minuscola si definisce come costante individuale. La lettera predicativa sta per la proprietà predicata all'individuo, mentre la costante individuale per l'individuo stesso.
Si può compiere la stessa operazione con le relazioni.
Se prendo l'enunciato "Tizio ha ucciso Caio" posso tradurlo in questo modo: Utc. La cosa importante, in questo caso, è tenere presente bene l'ordine degli elementi, ossia delle costanti individuali.
Frege si è spinto ancora oltre: ha matematizzato i quantificatori.
Un quantificatore viene inteso da Frege come una funzione di secondo grado. Il quantificatore come funzione non si applica più semplicemente alle costanti individuali, ma alle lettere predicative stesse.
Esistono due tipi di quantificatori: l'universale e l'esistenziale.
Il quantificatore universale sta per "per ogni x" e indica la totalità di elementi con una certa proprietà. Il quantificatore esistenziale indica uno o più elementi con una certa proprietà e sta per "esiste una x". Alcuni esempi:

2) Quantificatore esistenziale:

Come faccio a sapere se un enunciato è vero o è falso, ossia se è 1 o 0, nella logica predicativa?
Nel caso del semplice enunciato soggetto/predicato o di relazione, è sufficiente sapere se la costante individuale è un elemento dell'insieme dato dalla lettera predicativa.
Freud, in pratica, deve essere elemento dell'insieme degli psicanalisti.
Il caso dei quantificatori è più complesso.

Vediamo meglio la questione: che cos'è un modello logico?
Un modello è composto da un dominio non vuoto e da una funzione di interpretazione che assegna ad ogni costante individuale un elemento nel dominio e ad ogni lettera predicativa un insieme nel dominio.
In pratica il modello è ciò che ci permette di interpretare qualsiasi enunciato della logica.
Quando ho un enunciato che contiene un quantificatore universale devo chiedermi se ogni elemento nel modello soddisfa quell'enunciato.
Per esempio se dico: "Tutte le cose che esistono sono state create", in questo caso sto dicendo che se questo enunciato è vero, allora l'insieme delle cose create coincide con il dominio del modello.
Fin qui sembra tutto semplice, ma cosa dire quando mi trovo di fronte ad un argomento come questo:
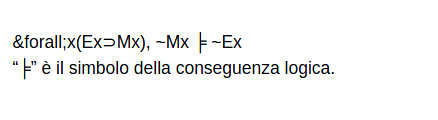
Una formula è conseguenza logica di un dato insieme di formule se in ogni modello, ogni assegnazione che soddisfa quell'insieme di formule soddisfa anche quella formula.
In questo caso abbiamo come insieme di formule:

Questo significa che l'argomento dice: per ogni x, se x è esteso, allora è materiale, ma x non è materiale, dunque non è esteso. Ci rendiamo immediatamente conto che questo enunciato è vero a seconda di cosa sostituiamo alla x. Se mettiamo una scimmia, per esempio, la scimmia è materiale. Se mettiamo il fantasma del padre di Amleto, lui non è materiale.
Tuttavia bisognerebbe anche capire se è vero che non vi sono cose che sono materiali e non sono estese,
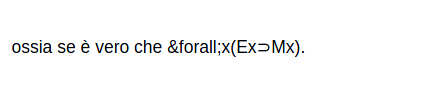
Se sono vere le premesse, in pratica, se la conclusione deriva dalle premesse, allora la conclusione deve essere vera.
Problema: possiamo prendere tutte le formule e capire se sono valide, ossia conseguenza logica di un insieme di altre formule, di modo tale da creare un insieme delle formule valide e uno delle formule non valide?
Se fosse possibile trovare un metodo per decidere per ogni formula se è valida, ossia conseguenza logica di un insieme di formula, allora la logica predicativa sarebbe decidibile.
Quello che ha dimostrato Alan Turing è che, in realtà, la logica predicativa non è affatto decidibile.
Nel pensare questo Alan Turing ha pensato una macchina che doveva risolvere questo problema, questa macchina è poi diventata il primo modello di computer: l'A.C.E. (Automatic Computer Engine).
Il computer di Turing è detto anche macchina di Turing.
La macchina di Turing legge ed esegue programmi.
La macchina, una volta dato un input, deve dare una risposta come output, se non può rispondere va in un loop, ossia continua a girare a vuoto.
Per provare a spiegarvi come funziona grossomodo una macchina di Turing mi servirò di un capitolo dell'opera Mente, linguaggio e realtà di Hilary Putnam.
I programmi che la macchina deve leggere sono tutti scritti su un nastro.
Il nastro è composto di caselle e su ogni casella è stampato un simbolo. La macchina ha un meccanismo di lettura per leggere il simbolo nella casella del nastro e legge una casella alla volta. Inoltre la macchina è in grado cancellare il simbolo nella casella letta e di stamparne un altro sulla stessa casella.
Il filosofo Putnam descrive la macchina di Turing attraverso una tavola di transizione.
Questa tavola è composta di righe e di colonne. Nelle righe troviamo quei famosi simboli: s1, s2, s3 , s4, ecc. Nelle colonne troviamo degli stati: A, B, C, D, ecc. Nella tabella un simbolo è legato ad uno stato tramite un'istruzione: S, C, D, ecc. Putnam fa tre esempi:
1) s5SA (stampa il simbolo s5 nella casa che leggi adesso, poi passa alla successiva e vai in stato A)
2) s7CB (C significa: continua a leggere la stessa casella)
3) s3DC (D significa: leggi la casella immediatamente a destra).
Per spiegare in pratica come funziona la macchina di Turing, Putnam ci offre questo esempio pratico: supponiamo di avere un nastro con scritto "11 + 111"; ogni simbolo corrisponde ad una cella del nastro; la macchina legge la prima cella e vede 1; la macchina esegue la somma sostituendo "+" con "1" e cancellando il primo "1"; dunque la macchina stampa "11111".
È chiaro che qui la macchina tratta questi numeri come delle stringhe. Infatti 11 + 111 = 122, ma "11" +"111" = "11111".
Provate a scrivere con Javascript questo codice:
var num1 = "22";
var num2 = "22";
var result = num1 + num2;
document.write(result);
Se avrete eseguito bene il codice nel browser vi comparirà come risultato 2222. Questo perché 22 è un numero, ma "22" è una stringa, dunque è considerata come insieme di simboli e basta, non in senso quantitativo.
Alan Turing con il teorema dell'indecidibilità ha dimostrato che se ponessimo quel problema di logica ad un computer, il computer entrerebbe in un loop e non ci darebbe nessuna risposta.
Io, invece, spero di aver dimostrato come l'informatica, in realtà in parte discenda dalla filosofia, in particolare dalla logica filosofica e dalle prime calcolatrici.
