La logica predicativa e modale con possibili applicazioni

∀
La logica enunciativa ha una storia che precede la filosofia analitica e che risale agli stoici.
Alla filosofia analitica, che spesso viene identificata con una certa visione logica e argomentativa della filosofia, vanno piuttosto attribuite altre forme di logica: la logica predicativa e la logica modale.
La logica predicativa nasce con Gottlob Frege, che è considerato il padre della filosofia analitica.
La logica modale, invece, va attribuita a Saul Kripke, altro filosofo analitico.
Se la filosofia analitica viene associata alla logica, non significa che chi non sia analitico non si interessi di logica e soprattutto non argomenti, ma è certamente vero che con la filosofia analitica sono avvenuti i maggiori progressi in ambito logico e che gli analitici nell'argomentare usano metodi più chiari come la scrittura canonica dell'argomento.
È da precisare che la logica degli analitici è principalmente quella predicativa, ma che non tutti gli analitici sono d'accordo con la logica modale, per esempio Willard van Orman Quine non segue la logica modale.
Ho intenzione di presentare le logiche degli analitici come primo tentativo di fondare la filosofia come scienza su basi matematiche, perciò vorrei analizzare questo tentativo e in un secondo momento spiegare le sue falle.
La logica non è solo usata per capire se un argomento è corretto o meno, di fatto gli analitici operano con la logica in tantissimi settori: volevano fondare la matematica sulla logica (Russell), hanno pensato un'epistemologia in termini formali (Carnap), hanno usato la logica per fare filosofia del linguaggio e analisi degli enunciati (Wittgenstein), più recentemente hanno pensato di formalizzare anche la fenomenologia (Eduard Marbach) e altro ancora.
Comincerò presentandovi la logica predicativa almeno nei suoi fondamenti.
Non parlerò del calcolo logico predicativo, parlerò della formalizzazione degli enunciati, di che cos'è un modello e del sistema della logica predicativa con qualche teorema. Frege, come ho detto, è il padre della logica predicativa.
Egli ha avuto un'intuizione geniale: pensare un enunciato come una funzione. Mentre nella logica enunciativa una proposizione come "Socrate è un uomo" si formalizza semplicemente con la una lettera (U), nella logica predicativa è possibile analizzare la struttura interna della proposizione.
La funzione segue la formula: f (y) = x, un esempio di funzione è la seguente S (1) = 2, dove S sta per "successore" e il successore di 1 è 2. In questo modo possiamo formalizzare la proposizione precedente in questa maniera: Us. U sta per "uomo", s sta per Socrate. La lettera maiuscola è la lettera predicativa, la lettera minuscola è la costante individuale.
Nella logica predicativa si usano le prime lettere dell'alfabeto per le costanti individuali (a, b, c, d, ecc.) e le ultime per le variabili (x, y, z, v, ecc.). In questo modo posso formalizzare una qualsiasi proposizione soggetto/predicato, ma posso formalizzare anche una relazione.
Nel caso della relazione i termini della relazione vanno messi nel giusto in ordine, se si tratta di una relazione asimmetrica cambiare l'ordine, infatti, cambierebbe il significato.
Ad esempio una proposizione come "Tizio è più alto di Caio" si formalizza in questo modo: Atc (A = essere più alto di, t = Tizio e c = Caio). I valori delle funzioni sono 1 e 0, che sono vero e falso. Se è vero che "Tizio è più alto di Caio", allora Atc = 1.
Anche nella logica predicativa ci sono gli stessi connettivi della logica enunciativa:

La logica predicativa ci permette inoltre di formalizzare i quantificatori di Aristotele.
Aristotele distingueva il generale dal particolare.
Un giudizio generale è "Tutti i delfini sono dei pesci", un giudizio particolare è "Alcuni gatti hanno il pelo nero".
Frege ha pensato i quantificatori come funzioni di secondo livello. Il generale è rappresentato dal quantificatore universale (per ognix), mentre il particolare da quello esistenziale (∃x).
In questo modo si possono formalizzare i miei due esempi: per ognix (Dx ⸧ Px), dove D sta per "delfino" e P per "pesce"; ∃x (Gx ∧ Nx), dove G sta per "gatto" e N per "avere il pelo nero".
Notate la differenza con le negazioni: ~ per ognix (Dx ⸧ Px) significa che non tutti i delfini sono dei pesci; ~ ∃x (Gx ∧ Nx) significa che non esistono gatti con il pelo nero. Questo mostra che i quantificatori sono intercambiabili, infatti ~ ∃x (Gx ∧ Nx) ↔ per ognix (Gx ⸧ ~ Nx), oppure ~ per ognix (Dx ⸧ Px) ↔ ∃x (Dx ∧ ~ Px).
Con il quantificatore universale si usa sempre il condizionale, mentre con quello esistenziale si usa sempre la congiunzione.
Ogni linguaggio ha una semantica e una sintassi, la semantica riguarda il significato dell'enunciato, mentre la sintassi riguarda la struttura dell'enunciato.
La semantica nella logica è definita nei termini della conseguenza logica (╞): si dice che se una formula è conseguenza logica di una serie di formule le stesse assegnazioni che soddisfano quelle formule soddisfano anche questa formula.
Se una conclusione è conseguenza logica delle premesse, non può essere che le premesse sono vere e la conclusione è falsa.
La semantica del linguaggio logico è pensata a partire dalla costruzione di un modello.
Il modello ci permette di dare un significato alle nostre espressioni che usiamo.
Nel caso della logica predicativa il modello funziona in questo modo:
il modello comprende un dominio e una funzione di interpretazione;
il dominio è un insieme non vuoto;
la funzione di interpretazione ci permette di assegnare ad ogni costante individuale un elemento del dominio e per ogni lettera predicativa un insieme nel dominio;
quando abbiamo a che fare con una variabile bisogna assegnare alla variabile un elemento del modello, ma la stessa variabile può essere sostituita con altri elementi (in questo caso si parla di x-varianti).
Alfred Tarski, logico e filosofo analitico, ha pensato la verità nella logica predicativa nei termini della soddisfazione di una formula e questo metodo è quello che viene usato di fatto.
Una formula come Pa, dove a è Aristotele e P è filosofo, è vera se e solo se nel modello a appartiene all'insieme P.
Il caso più complesso è quello dei quantificatori:
nel caso del quantificatore universale se tutti gli oggetti del modello soddisfano una data formula, allora è vera la formula (se dico per ognix (Dx ⸧ Px), se ogni oggetto che ha la proprietà D nel modello ha anche la proprietà P, allora la formula è soddisfatta, ossia è vero che tutti i delfini sono dei pesci);
nel caso del quantificatore esistenziale basta che vi sia almeno un oggetto perché la formula sia soddisfatta (se dico ∃x (Gx ∧ Nx), se esiste almeno un oggetto in un modello tale che ricade sotto l'insieme G e l'insieme N, ossia ha tutte e due le proprietà, allora la formula è soddisfatta, ossia è vero che ci sono gatti col pelo nero).
La sintassi è espressa nella logica predicativa con la nozione di derivabilità: una formula è derivabile da una sequenza di formule se e solo se quella sequenza di formule istanza uno degli assiomi o è derivabile dal modus ponens.
Gli assiomi della logica predicativa sono i tre della logica enunciativa più altri quattro. Ecco i sette assiomi:

Il caso più interessante è l'assioma 4, il quale ci permette di sostituire la variabile con un termine, tranne quando la formula è chiusa. Se prendo per ogniy(Px)tx, se metto come termine t la costante individuale a ottengo per ogniyPa, ma ci metto la y ottengo una formula chiusa.
Grazie alla logica predicativa posso formalizzare il sillogismo di Aristotele in questo modo:
per ognix (Ux ⸧ Mx), Us ├ Ms
(U = uomo, M = mortale, s = Socrate)
Per ogni x, se x è un uomo, allora x è mortale; Socrate è un uomo; dunque Socrate è mortale.
Posso formalizzare argomentazioni con la logica predicativa, avendo il vantaggio di poter studiare la struttura interna dell'enunciato e posso dire se una certa argomentazione è corretta oppure no. Inoltre è possibile dimostrare dei teoremi. Faccio un esempio di dimostrazione:
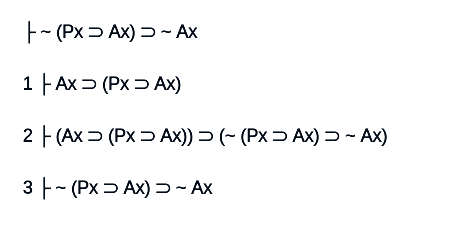
La logica predicativa è composta di molte altre cose di cui non parlerò:
il calcolo logico predicativo;
teoremi complessi e famosi come il teorema della completezza di Gödel o il teorema Löwenheim-Skolem;
formalizzazioni aritmetiche come l'aritmetica di Peano; molto altro ancora.
Quella che di cui ho parlato è una logica di primo ordine, ossia una logica in cui la variabile è usata solo per le costanti individuali. Una logica di primo ordine può aggiungere altri simboli come quello dell'identità (=), ma è importante sapere che ci sono anche le logiche di alto ordine, nelle quali la variabile vale anche per le lettere predicative, ad esempio: per ognixXx.
Oltre alla logica predicativa gli analitici hanno pensato anche una logica modale, in particolare Saul Kripke. La logica modale aggiunge alla nozione di modello quella di mondo possibile.
Ci sono due tipi di logica modale:
la logica modale enunciativa e la logica modale predicativa.
La logica modale aggiunge questi due simboli al linguaggio:
◊ (simbolo della possibilità) Esempi: è possibile che Marco stia dormendo (◊ D); è possibile che la macchina di Pietro sia rossa (◊ Sm)
□ (simbolo della necessità) Esempi: è necessario che l'inversione degli addendi non cambi la somma (□ I); è necessario che ogni uccello sia pennuto (□ 𐆗x (Ux ⸧ Px) )
Nella semantica della logica modale si deve tenere conto anche dei mondi possibili, in quanto un enunciato risulta vero rispetto ai mondi possibili considerati.
Una formula come ◊ D è vera se almeno in qualche mondo possibile l'enunciato è vero, basta infatti che vi sia almeno un mondo possibile in cui Marco stia dormendo. Una formula come □ I è vera se vale per ogni mondo possibile, ossia non esiste un mondo in cui invertendo l'ordine degli addendi la somma cambia.
Gli operatori della logica modale sono intercambiabili, infatti: ◊ D ↔ ~ □ ~ D; □ I ↔ ~ ◊ ~ I. Ci sono diversi sistemi nella logica modale, il più avanzato è S5 ed è stato pensato da Clarence Irving Lewis. Questo sistema ha quattro assiomi:

Un'altra regola importante è quella della necessitazione: se α è un teorema, allora □ α. Anche qui nella logica modale esiste una forma di calcolo.
La logica modale è oggi usata dagli analitici in numerosi ambiti tra cui la metafisica e la mereologia.
Ci sono diversi usi che si possono fare della logica, vorrei parlare di un modello formale che è stato pensato da Marbach per la fenomenologia in ambito analitico.
Ogni percezione è percezione di qualcosa, questo è il carattere di intenzionalità dell'atto di coscienza. In genere la percezione è di un oggetto, un oggetto particolare. Volendo formalizzare l'oggetto verrà pensato in termini formali con una variabile (x).
Perciò una singola percezione è scritta nel linguaggio di Marbach come: (PER)x. Questa formula vale per la percezione presente, ma se vogliamo riferirci ad una ripresentazione di una percezione passata allora scriveremo: [PER]x.
Marbach complica la formula inserendo la nostra credenza che un certo evento sia accaduto nel passato in questo modo: (REP p ├ [PER])x. In queste formule compaiono alcuni simboli logici e sono un tentativo di formalizzare il linguaggio della fenomenologia.
Lo strumento matematico della logica quindi è sufficientemente potente da permettere di essere utilizzato non solo per studiare la forma e la correttezza di determinati argomenti, ma anche per qualsiasi altra cosa, laddove la formalizzazione matematica torna utile.