La matematica del virtuale: Gilles Deleuze secondo Manuel DeLanda

Gilles Deleuze è un filosofo francese, uno dei maggiori esponenti del poststrutturalismo.
Di solito i suoi libri sono molto amati perché Deleuze scrive bene e ha una scrittura davvero accattivante, tuttavia la maggior parte dei suoi libri sono poco chiari e forse del tutto incomprensibili ai più.
Il fatto è che Deleuze, filosofo onnivoro in fatto di letture, possedeva conoscenze negli ambiti del sapere più disparati (neuroscienze, termodinamica, biologia, matematica, letteratura, musica, cinema, economia, filosofia, ecc.).
Oltretutto Deleuze non spiega mai veramente tutto quel che cita, mentre sembra sempre presupporre che il lettore sappia e conosca tutti quegli ambiti disciplinari a cui lui si riferisce.
Deleuze ha introdotto nella filosofia continentale temi matematici completamente nuovi come: la varietà riemaniana; il differenziale; la teoria delle singolarità; la topologia; la teoria del caos; i frattali.
Parlerò di questi temi, in parte usando come riferimento Gilles Deleuze, ma soprattutto seguendo la lettura della matematica in Deleuze da parte del filosofo Manuel DeLanda nello scritto Intensive science and virtual philosphy.
Partirò da concetti generali per poi addentrarmi nella teoria del virtuale di Deleuze, che è il luogo in cui Deleuze ha maggiormente applicato la matematica.
Una chiara interpretazione della teoria del virtuale ci è fornita dallo stesso Manuel DeLanda, perciò farò molto uso di questa versione.
Tre concetti chiave e importantissimi in Deleuze per quel che riguarda la matematica sono questi: molteplicità; singolarità; differenziale.
Ognuno di questi concetti risponde ad un problema filosofico:
la molteplicità vorrebbe superare il vecchio problema Uno/molti;
il concetto di singolarità deve rimpiazzare il millenario concetto di essenza;
i differenziali dovrebbero spiegarci il divenire.
Ognuno di questi termini è collegato agli altri: le cose si definiscono per distribuzione di singolarità che sono molteplicità; la molteplicità e il differenziale confluiscono nella geometria differenziale di Riemann.
Partiamo pure dal concetto di differenziale nella matematica.
Manuel DeLanda definisce il differenziale come relazione tra due cambiamenti di quantità.
Un esempio di DeLanda in cui si applica il differenziale è il calcolo della velocità di un proiettile prima che colpisca la testa di un soggetto e questo muoia. Russell cita il caso della palla lanciata in aria quando raggiunge il punto più alto e sta per ricadere per terra. DeLanda cita altri esempi come il fiore che sboccia. In ogni caso il differenziale sembra essere correlato ad un cambiamento di stato, ossia al divenire.
DeLanda definisce il differenziale come velocità del divenire (speed of becoming).
Per spiegare in cosa consista un differenziale torno al caro Gustavo Bessière.
Bessière è partito con la spiegazione di una funzione, dopo è passato alla spiegazione della derivata e alla fine arriva al differenziale. Se prendo una candela accesa, la candela più brucerà, più si consumerà e quindi scenderà in altezza.
Posso esprimere questo fatto semplicemente dicendo che la sua altezza diminuisce in funzione del suo bruciare. Posso pensare che la candela dimezzi la sua altezza ogni volta che brucia un tot. tempo, perciò posso esprimere questo con la funzione y = - 2x.
La derivata è uguale alla quantità della crescita o della diminuzione calcolata per ogni punto della funzione, quindi, in questo caso pensando che la diminuzione d'altezza è costante, la derivata è
y'= - 2.
In generale la derivata è calcolata come y' = axa-1.
Il differenziale non è altro che la derivata, è come un altro modo di calcolare la derivata. Il differenziale si esprime con questa formula: dy/dx. Dy, spiega Bessière, è il differenziale di y, ossia l'incremento di y; dx, invece, è il differenziale di x, ossia l'incremento di x. x e y sono sempre ascisse e ordinate, sono sempre i simboli usati nel piano cartesiano.
Se il differenziale non è altro che la derivata, questo significa che dy/dx = y', perciò possiamo ricavare le seguenti formule:
1) dy = y'dx
2) se y = ax, allora y + dy = a (x + dx).
Seguendo l'esempio di Bessière immaginiamo un albero che cresce di 2 metri ogni anno. In x poniamo l'età e in y l'altezza. Supponendo la grandezza costante, avremo una funzione lineare che cresce di 2x, perciò la funzione è di y = 2x.
Prendendo la nostra funzione obliqua, se consideriamo l'anno 2, l'altezza sarà 4, l'anno successivo (3) l'altezza sarà 6.
Tracciando una linea orizzontale nelle x che incontra il punto y = 4, per x =2, prolungandola fino al punto corrispettivo sulla stessa linea rispetto alla x per quanto riguarda l'anno successivo, abbiamo dx = 1.
La verticale che parte da quel punto (y = 4; x =3) e raggiunge la funzione in un altro punto (y = 6 ; x = 3) è dy, perciò dy = 2. Dunque dy/dx = 2/1, perciò dy =2dx.
Cito un passaggio in cui Deleuze parla di differenziali:
«Dx è assolutamente indeterminato in rapporto a x, dy in rapporto a y, ma essi sono perfettamente determinabili l'uno in rapporto all'altro, e questo chiarisce perché un principio di indeterminabilità corrisponde all'indeterminato come tale.
L'universale non è un nulla, in quanto, secondo l'espressione di Bordas, si danno "rapporti dell'universale". Dx e dy sono assolutamente indifferenziati, nel particolare come nel generale, ma assolutamente differenziati nel e mediante l'universale.
Il rapporto dy/dx non è come una funzione che si stabilisca tra quanta particolari nell'intuizione, ma non è neppure un rapporto generale tra le grandezze variabili o quantità algebriche.
Ciascun termine non esiste in assoluto se non nel suo rapporto con l'altro, in quanto non occorre né è più possibile indicare una variabile indipendente.» (Deleuze, Gilles, Differenza e ripetizione, Cortina, Milano, 1997, p.224-225)
Il differenziale potrebbe essere molto utile in ambito filosofico per studiare concetti come il concetto di divenire e mutamento. In fondo il differenziale misura allo stesso modo della derivata, ma in modo diverso, l'incremento o la diminuzione.
Quando l'albero cresce, un'auto percorre x kilometri in un certo tempo, in tutti questi casi si parla di un mutamento. Il differenziale ci permette di studiare matematicamente dei mutamenti simili.
I differenziali hanno cambiato profondamente la matematica. Ricordo che uno dei più importanti studiosi sui differenziali era Leibniz, ossia un filosofo. Grazie al differenziale è stato possibile studiare la geometria non più facendo uso degli assi cartesiani. In questo modo è nata la geometria differenziale.
Gauss è forse uno dei padri della geometria differenziale.
Gauss sviluppa un metodo per impiantare le assi coordinate sulla superficie stessa della figura. Una volta che i punti sono diventati numeri si usa il calcolo differenziale. Morris Kline, storico della matematica spesso citato da Manuel DeLanda, afferma che per Gauss la superficie è lo stesso spazio.
Gauss studia il caso delle figure curve a due dimensioni. La geometria differenziale rientra nelle geometrie non-euclidee, per studiare la geometria differenziale conviene studiare prima bene le parametriche (superfici parametriche e curve parametriche).
Seguendo Morris Kline su Gauss, gli studi di Gauss partono dai lavori di Eulero, in particolare Kline cita l'applicazione delle parametriche (u, v) di Eulero per rappresentare i punti della superficie.
Così abbiamo per le tre variabili della geometria di Cartesio le seguenti equazioni:
x = x(u, v); y = y(u, v); z = z(u, v).
u e v sono di fatto dei vettori.
Le coordinate così come le ho scritte sono tipiche di una superficie parametrica o superficie differenziabile. Usando i determinati di matrici si possono studiare le curve guassiane.
Un esempio si può fare utilizzando una semplice matrice 2 x 2.
In generale il determinante di questa matrice è:
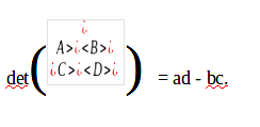
Per una funzione come f (x,y) = ax2 + bx2, il suo determinante è 4ab. Infatti b = 0 e c = 0, mentre a = 2a e b = 2b. In termini di differenziali le formule di Eulero, come mostra Kline, per Gauss diventano:
dx = a du + a' dv; dy = b du + b' dv; dz = c du + c' dv.
Nelle superficie curve Gauss, studiando la nozione di curvatura di superficie, calcola l'arco infinitesimale servendosi di Pitagora. La curva (ds) viene calcolata da Gauss con questa formula:
ds2 = dx2 + dy2 + dz2
Riprendendo le formule precedenti (le equazioni di Eulero e le trasformazioni differenziali di queste), Moriss Kline mostra in che modo Gauss converte la formula della curva:
ds2 = E(u, v) du2 + 2F(u, v) du dv + G(u, v) dv2
Usando i determinati Kline mostra che le equazioni corrispondenti alle lettere E, F, G.
E = a2 + b2 + c2; F = aa' + bb' + cc'; G = a'2 + b'2 + c'2
Con le formule che ho citato si ottiene la prima forma fondamentale di Gauss, questa forma non è altro che un determinante di questo tipo:
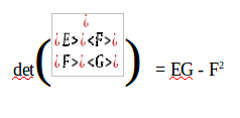
Morris Kline spiega inoltre la famosa curva gaussiana o curvatura totale, usando questa formula:
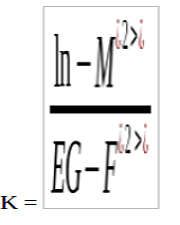
Il degno successore di Gauss nella geometria differenziale è chiaramente Bernhard Riemann.
Riemann si occuperà dello spazio n-dimensionale, definito solo dalla sue caratteristiche intrinseche e detto anche "varietà riemaniana".
Lo spazio di Riemann non richiede l'aggiunta di una dimensione ulteriore, esso è: n - 1.
A Deleuze della "varietà" interessa il carattere molteplice delle sue dimensioni e l'assenza di una dimensione maggiore. Mai più lo spazio trascendente di Cartesio.
Morris Kline spiega che il punto di una verità a n-dimensioni è rappresentato dai valori speciali assegnati a n parametri variabili (x1, x2, x3, x4, ecc.), l'aggregato di questi punti costituisce la verità n-dimensionale.
Si parla ad esempio di superficie di Riemann, questo è un esempio di varietà ad una sola dimensione.
Un arco infinitesimale è calcolato da Riemann con questa formula:
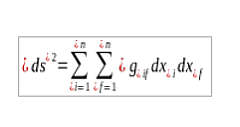
Deleuze fa spesso riferimento a Berhard Riemann, principalmente usa la nozione di varietà di Riemann per concepire il concetto filosofico di molteplicità (da non confondere con il molteplice).
Una definizione di molteplicità in Deleuze è la seguente:
«Il molteplice bisogna farlo, non aggiungendo sempre una dimensione superiore, ma al contrario il più semplicemente possibile, a forza di sobrietà, al livello delle dimensioni di cui si dispone, sempre n - 1 (l'uno fa parte del molteplice solamente così, venendo sottratto). Sottrarre l'unico dalla molteplicità da costituire. Scrivere in n - 1. Questo sistema potrebbe essere chiamato rizoma.» (Deleuze, Gilles, Guattari, Félix, Mille piani, Castelvecchi, Roma, 2010, p.51)
In Deleuze su Riemann si legge:
«Quando il matematico Riemann strappò il molteplice al suo stato di predicato per farne un sostantivo, "molteplicità", fu un avvento decisivo. Era la fine della dialettica a profitto di una tipologia e di una topologia delle molteplicità.
Ogni molteplicità veniva definita da n determinazioni, ma talvolta le determinazioni erano indipendenti dalla situazione, talaltra ne dipendevano. Per esempio, si può paragonare la lunghezza della linea verticale tra due punti alla lunghezza della linea orizzontale tra due altri: si vede qui che la molteplicità è metrica, nello stesso tempo in cui si lascia striare e in cui le determinazioni sono dette lunghezze. In compenso non si può comparare la differenza tra due suoni di altezza uguale e intensità distinta con due suoni di intensità uguale e altezza distinta.» (Deleuze, Gilles, Guattari, Félix, Mille piani, Castelvecchi, Roma, 2010, p.572)
Con queste analisi sulla geometria Deleuze studia il rapporto tra lo spazio non-metrico e quello metrico, spiegando come dal primo si possa generare il secondo.
Nella filosofia di Deleuze lo spazio non metrico è lo spazio liscio, mentre lo spazio metrico è lo spazio striato. Attraverso la striatura, ossia una metrizzazione dello spazio, è possibile, secondo Deleuze, passare dallo spazio liscio a quello striato.
Deleuze considera il matematico Benoit Mandelbrot come il matematico dello spazio liscio.
A Mandelbrot dobbiamo sicuramente gli studi sui frattali.
Mandelbrot usava i frattali per studiare cose come la forma geometrica della costa del Regno Unito. Famoso è anche l'insieme Mandelbrot, utilizzato nella topologia.
Deleuze usa i frattali per tante cose, in particolare per spiegare la natura della monade di Leibniz.
Secondo Deleuze la monade è molteplicità. Lebniz, spiega Deleuze, divide il continuo piegandolo, esattamente come accade nei frattali. In questo modo la monade è origami: piega della piega, della piega, della piega, ecc.
Due esempi di frattali di Deleuze sono: la curva di von Koch; la spugna di Sierpinsky. Nella curva di von Koch una linea retta viene piegata per formare sempre più triangoli, triangoli su triangoli. La Spugna di Sierpinsky è un grande cubo con tanti cubi interni all'infinito. La monade è un altro modo di vedere la molteplicità.
La molteplicità diventa, spiega Manuel DeLanda, nella teoria dei sistemi dinamici, lo spazio degli stati possibili che un sistema fisico può avere.
Primo passaggio: capire il numero dei modi in cui un oggetto può mutare, questi modi si chiamano gradi di libertà.
DeLanda fa due esempi: nella dinamica il pendolo può cambiare solo nella sua posizione e nel suo slancio; la bicicletta ha 10 gradi di libertà. Il pendolo abbisogna di un piano a due dimensioni, mentre la bicicletta uno spazio a 10 dimensioni.
A questo punto il singolo oggetto diventa un punto nella molteplicità ed è chiamata spazio di stato. Un fisico può studiare il cambiamento di un comportamento studiando il comportamento delle traiettorie in questi spazi.
Questo metodo cerca di catturare il modo in cui mutano le proprietà, catturare un processo. L'oggetto a molte dimensioni diventa un punto, ma lo spazio diventa sempre più complesso perché deve rappresentare tutte le dimensioni o i grandi di libertà.
Il secondo concetto essenziale in Deleuze è il concetto di singolarità.
Deleuze intende usarlo per compiere una svolta epocale in filosofia: rimpiazzare il vecchio concetto di essenza.
L'essenza è una sequenza di proprietà che l'ente possiede e che definisce l'ente per quello che è.
L'essenza è come una struttura, che ha il carattere di archetipo o forma ideale della cosa. Un tavolo è un tavolo, secondo la teoria delle essenze, poiché istanza l'essenza del tavolo.
Oggi non si usa più il termine essenza o universale in filosofia, ma spesso si sente usare la parola "type", tuttavia basti sapere che sono la stessa cosa.
Deleuze rimpiazza il vecchio concetto di essenza con la singolarità e mentre la singolarità nella scienza è un concetto usato prevalentemente in matematica o in fisica, lui lo applica in tantissimi ambiti.
Deleuze sulle singolarità:
«Cos'è un evento ideale? È una singolarità. O piuttosto una insieme di singolarità, di punti singolari che caratterizzano una curva matematica, uno stato di cose fisico, una persona psicologica e morale. Sono punti di ritorno, di inflessione, ecc.; colli, nodi, focolai, centri; punti di fusione, di condensazione, di ebollizione, ecc.; punti di pianto e di gioia, di malattie e di salute, di speranze e di angoscia, punti detti sensibili.
Tali singolarità nondimeno non si confondono né con la personalità di colui che si esprime in un discorso, né con l'individualità di uno stato di cose designato da una proposizione, né con la generalità o l'universalità di un concetto significato dalla figura o dalla curva.» (Deleuze, Gilles, Logica del senso, Feltrinelli, Milano, 1975, p.53)
Henri Poincaré ha individuato certe caratteristiche topologiche delle molteplicità a due dimensioni, queste caratteristiche si chiamano: singolarità.
Le singolarità influenzano il comportamento agendo come attrattori per le traiettorie. La singolarità rappresenta un'intrinseca tendenza a lungo termine del sistema.
Alcune singolarità sono punti topologici, così lo stato finale è uno stato stazionario.
Un punto singolare giuda un processo che ha come risultato forme fisiche differenti come la sfera o il cubo (es. la bolla di sapone). In questo modo la forma sferica non è spiegata a partire dall'azione di forme ideali o strutture, ma a partire dalle singolarità.
Ci sono alcuni tipi di singolarità che sono di carattere ciclico, nel senso che attraggono traiettorie producendo come dei cicli.
DeLanda cita due casi: ciò che fa funzionare la radio è proprio una singolarità; ciò che fa funzionare il cuore, anche qui è una singolarità.
Le singolarità non sono mai attualizzate, perciò rimangono essenzialmente virtuali.
Per capire meglio: le singolarità sono dei punti, esse sono usate anche in fisica; quando l'acqua raggiunge i 100° bolle, quando invece arriva a grado 0° diventa ghiaccio; considerando questi come dei punti singolari, possiamo definire, ad esempio il ghiaccio, non a partire dalle sue proprietà, ma rispetto ad un punto singolare, ossia il grado 0°.
Tuttavia se consideriamo lo stato attuale dell'acqua liquido, dal punto di vista della teoria del virtuale, gli altri due stati hanno esistenza virtuale, perciò virtualmente vale che se l'acqua raggiungesse nella temperatura un dato punto singolare diventerebbe vapore acqueo.
Manuel DeLanda spiega che con un gruppo di trasformazioni si possono classificare le figure geometriche per le loro invarianti.
Il cubo non produce cambiamenti in un osservatore se ruotato di 90°, ma non se ruotato di 45°. La sfera si può ruotare quanto si vuole e non cambierà mai per l'osservatore.
Questo lo si esprime dicendo che la sfera ha più simmetria del cubo relativamente ad una trasformazione di rotazione. Il grado di simmetria è misurato dal numero di trasformazioni che lascia invariante una proprietà.
A differenza della teoria delle essenze le invarianti sono date solo a partire da un dato numero di trasformazioni. È possibile passare da una figura all'altra perdendo o guadagnando simmetria. Attraverso un processo di rottura di simmetria la sfera può diventare un cubo.
Nei processi fisici una rottura di simmetria è una fase di transizione.
Questi fenomeni accadono a seguito di valori critici (es. temperatura). L'acqua a determinate temperature diventa ghiaccio (0°) o vapore acqueo (100°). Un gas ha maggiore simmetria di un solido e diventa solido attraverso un processo rottura di simmetria.
Una singolarità può entrare in un processo di rottura di simmetria ed essere convertita in un'altra, queste transizioni sono dette biforcazioni.
Le biforcazioni si possono studiare aggiungendo allo spazio di stato uno o più parametri di controllo che determinano la forza delle perturbazioni alle quali il sistema è soggetto.
Questi parametri di controllo mostrano valori critici, soglie di intensità nelle quali ha luogo una biforcazione rompendo la simmetria del sistema.
Si parla di biforcazione quando si ha un cambiamento nei punti di equilibrio di un sistema o nella loro stabilità. I valori attraverso i quali si producono tali cambiamenti sono detti valori critici.
Un cambiamento di questo tipo può portare ad una catastrofe.
Il concetto di biforcazione, spesso usato da Deleuze, è molto impiegato nella teoria del caos. In particolare sono tipiche della teoria la biforcazione di Hopf o la biforcazione a nodo sella.
Deleuze si interessava di teoria del caos e ha letto il famoso matematico René Thom, matematico noto per la teoria delle catastrofi.
Partendo da un punto di attrazione, in un punto critico di un parametro di controllo diventa instabile e biforca in un attrattore periodico. Con altre biforcazioni e valori critici si può ottenere un attrattore caotico.
Manuel DeLanda definisce le molteplicità come universali concreti, Deleuze pensa le molteplicità in uno spazio continuo in cui sono collegate.
«Principio di molteplicità: il molteplice solo quando è effettivamente trattato come sostantivo, molteplicità, non manifesta alcun rapporto con l'Uno come soggetto o oggetto, come realtà naturale o spirituale, come immagine e mondo.
Le molteplicità sono rizomatiche ed evidenziano la loro distanza dalle pesudo-molteplicità arborescenti. Non esiste alcuna unità che faccia da perno nell'oggetto o si divida nel soggetto, nessuna unità neanche per abortire nell'oggetto o per "ritornare" nel soggetto.
Una molteplicità non ha né soggetto né oggetto, ma soltanto determinazioni, grandezza, dimensioni che non possono crescere senza che essa cambi natura (le leggi di combinazione crescono allora con la molteplicità).» (Questo sistema potrebbe essere chiamato rizoma.» (Deleuze, Gilles, Guattari, Félix, Mille piani, Castelvecchi, Roma, 2010, p.53)
Questo fenomeno della simmetria serve a DeLanda per spiegare quel fenomeno che Deleuze definisce con il termine "differenziazione".
La differenziazione è quel processo che spiega il passaggio dal virtuale all'attuale.
Passo dopo passo Manuel DeLanda fa emergere una matematica del virtuale e cerca di spiegare con i concetti che mano a mano sto presentando della matematica, concetti che usava lo stesso Deleuze, il passaggio dalla realtà virtuale a quella attuale.
Così infatti fa DeLanda sfruttando la differenza tra lo spazio metrico e quello non metrico, sfruttando, cioè, la gerarchia esistente tra le varie geometrie sviluppate fino ad ora.
Nella geometria euclidea si usano lunghezze e distanze fissate. Concetti come lunghezza, volume e area sono detti metrici. Lo spazio euclideo è conosciuto come spazio metrico.
Tuttavia esistono spazi in cui le distanze non sono fissate, questi sono spazi non-metrici.
Si può pensare gli spazi metrici come prodotti a partire da una differenziazione con rottura di simmetria a partire dagli spazi non metrici, questo è quello che pensa DeLanda.
In determinate in geometrie, come quella differenziale, i concetti metrici non sono fondamentali. Ce ne sono altre: geometria proiettiva, geometria affine e topologia.
Felix Klein, famoso matematico, ha pensato una gerarchia delle geometrie.
DeLanda fornisce questi esempi: nella geometria euclidea il parallelismo e la linea retta rimangono invarianti, ma non la lunghezza; due triangoli nella geometria euclidea sono uguali se hanno lati uguali, ma nella geometria affine i triangoli non cambiano a seconda della lunghezza dei lati; in geometria euclidea due sezioni di coni per essere uguali devono essere dello stesso tipo e della stessa misura, mentre nella geometria affine basta che siano della stessa misura; siccome il triangolo, il quadrato e il cerchio possono essere deformati l'uno nell'altro, nella topologia diventano una e una sola figura.
La gerarchia delle geometrie dalla meno differenziata (metrizzata) è la seguente:
"topologia, geometria differenziale, geometria proiettiva, geometria affine, geometria euclidea".
In questo modo si può ottenere lo spazio metrico da quello non-metrico. È possibile paragonare, come fa DeLanda, il metrico/non-metrico all'estensivo/intensivo della termodinamica.
Nella termodinamica si distinguono due tipi di proprietà: le proprietà estensive e quelle intensive.
Un esempio di proprietà estensiva è la lunghezza.
Una barra di ferro può essere lunga due metri, se la barra di ferro viene divisa in due cambierà la lunghezza delle parti (1 metro), ma se la temperatura totale era di 90°, questa non si divide e rimane la stessa da entrambe le parti.
La temperatura è un esempio di proprietà intensiva.
La temperatura, o le proprietà intensive in generale, non possono essere divise senza che cambino di natura. L'acqua cambia di stato a certe temperature.
Tutti questi paragoni e questi passaggi di DeLanda sono, potremmo dire, suoi collegamenti tra branche scientifiche diverse, collegamenti che hanno il merito di spiegare come la teoria di Deleuze valga in generale e possa essere utile a varie branche della scienza.
Per spiegare la teoria del virtuale di Deleuze in poche parole, si potrebbe dire questo: il virtuale è una dimensione completamente indifferente alle opposizioni, la quale, attraverso un processo di differenziazione si attualizza in uno degli opposti.
Il virtuale è indifferente all'opposizione maschile/femminile, ma un processo di differenziazione fa sì che solo uno dei due opposti si attualizzi.
In generale la realtà in cui noi viviamo e che percepiamo è una realtà attuale, il virtuale riguarda le possibili traiettorie e storie che non si sono realizzate, ma che avrebbero potuto tranquillamente realizzarsi.
L'unità di base del virtuale secondo DeLanda in Deleuze è la molteplicità. La molteplicità è definita dalla distribuzione delle singolarità.
Il virtuale va visto come uno spazio non metrico o spazio continuo che si differenzia in se stesso.
Il virtuale deve spiegare l'individuazione. Le traiettorie rappresentano gli stati attuali nel mondo, mentre gli attrattori non sono mai attualizzati perché nessun punto delle traiettorie raggiungerà mai l'attrattore.
Le singolarità rappresentano le tendenze a lungo termine del sistema e mai il suo stato attualizzato. La stabilità delle traiettorie dipende dalla resistenza a piccoli shock.
La stabilità degli attrattori, spiega DeLanda, la si verifica sottoponendo il campo vettoriale a ulteriori perturbazioni, semplicemente aggiungendo un altro campo e vendendo cosa succede. A causa di una perturbazione può avvenire una biforcazione, la biforcazione è definita da una continua deformazione del campo vettoriale.
Definizione di molteplicità di DeLanda: "Una molteplicità è un insieme di vettori annidato correlati uno con l'altro da biforcazioni di rotture di simmetria, insieme con la distribuzione degli attrattori che definiscono ognuno dei suoi livelli incorporati. La molteplicità è virtuale. Le traiettorie hanno lo stato della possibilità".
DeLanda cita il pensiero di Ronald Giere relativamente alla logica modale.
Giere fa notare che le critiche alla logica modale, come le famose di critiche di Quine, dipendono dall'ambiguità del linguaggio, perché se dico "l'uomo calvo nel vano della porta" o "l'uomo grasso nel vano della porta", certamente con tutti questi mondi possibili e questi uomini nel vano della porta arrivo a considerazioni che appaiono assurde.
Tuttavia Giere, spiega DeLanda, crede che la logica modale dovrebbe pensare i mondi possibili non nel senso del mondo possibile in cui "Napoleone vince la battaglia di Waterloo", ma come possibili stati che la materia avrebbe potuto assumere e che nei fatti non ha assunto.
DeLanda spiega che la logica modale certamente tende all'essenzialismo, in quanto deve spiegare come può uno stesso individuo abitare tanti mondi possibili.
Questo problema, nota DeLanda, riguarda anche i fisici, per esempio quelli che credono negli universi paralleli, anche loro hanno questi problemi, problemi di natura filosofico-logica. In ogni caso DeLanda intende rimpiazzare le essenze con la storia singola dei singoli individui, che è ciò li definisce.
DeLanda, come Deleuze, non sono d'accordo con l'impiego della nozione di possibile. DeLanda afferma piuttosto che bisognerebbe pensare il virtuale come possibili traiettorie che avrebbe potuto prendere un determinato oggetto e che non ha preso.
Queste considerazioni potrebbero portare un giorno a ripensare la logica modale, magari si potrebbe costruire una logica corrispettiva per il virtuale.
Deleuze è un personaggio molto interessante in filosofia, oggi molto studiato, che ha dato fantastici contributi ad un maggiore uso della matematica nell'ambito filosofico.
Molti di questi studi dovrebbero diventare uno spunto nella filosofia per pensare modelli ontologici basati sulla matematica.
Foto Youtube, Pixabay