Andare oltre la logica classica

Penso sia da tempo che la filosofia si stia accorgendo dei limiti del modello logico formale utilizzato fino ad ora.

I continentali non hanno mai aderito alla visione degli analitici semplicemente perché non accettano la logica classica formale come unico modello di logica.

Oggi, sostiene Manuel DeLanda, ci sono anche dei filosofi analitici che stanno abbandonando la logica per orientarsi verso altri modelli matematici.

Un esempio di DeLanda è Ronald Giere, un filosofo analitico della scienza. Scrivo questo testo per spiegare quali sono i limiti della logica classica e le ragioni per le quali la logica classica non ci spiega molti fenomeni che pure sono di grossa importanza.

Inoltre vorrei cominciare a tratteggiare qualche strada alternativa rispetto alla logica classica. Un esempio di come la logica classica dei filosofi non funzioni in certi ambiti ci viene dalla fisica.

Ne parla ad esempio Amanda Gefter nel testo Due intrusi nel mondo di Einstein quando presenta le teorie della fisica Markopoulou. Nel libro si legge:

«Potremmo pensare che la logica sia la logica, eterna e inviolabile. Ma se ciò fosse vero, la logica ordinaria non avrebbe bisogno di un nome.

Un nome, invece, ce l'ha: logica booleana. Codificata in innumerevoli asserti "Se P, allora Q", che gli studenti di filosofia di tutto il mondo stavano mandando a memoria mentre noi parlavamo, la logica booleana è una logica binaria, la logica del sì e del no, del vero e del falso, del nero o del bianco.

Ma alla cosmologia quantistica sono necessarie scale di grigio - spiegava Markopoulou - per un fatto semplice ma di capitale importanza: la velocità della luce è finita. Ogni volta che osserviamo qualcosa, la luce deve andare dall'oggetto ai nostri occhi, e ciò non accade istantaneamente. Viaggia a 300.000 chilometri al secondo. La luce del Sole impiega otto minuti a raggiungere la Terra - guardare il Sole è come saltare in una macchina del tempo che ci riporta a otto minuti fa.

Se vi mettete a osservare le stelle, state guardando migliaia di anni indietro; afferrate un telescopio e potete vedere miliardi di anni nel passato. Ma il punto è il seguente: ci sono stelle la cui luce non ha ancora avuto abbastanza tempo dal Big Bang per raggiungerci . Voi aspettate, e alcune di queste stelle ce la faranno. Ma essendo la velocità della luce finita, ci saranno sempre porzioni di universo che non possiamo vedere.»

(Gefter, Amanda, Due intrusi nel mondo di Einstein, Cortina, Milano, 2015, p. 69-70)

Dal testo si deduce che Markopoulou sostiene una teoria dove l'universo è relativo all'osservatore e così è lo stesso per il vero e il falso.

Se Markopoulou come fisica quantistica considera la logica booleana o classica come del tutto inadeguata, è anche vero che non rompe completamente con la logica in generale, infatti sceglie di usare un altro modello di logica: la logica di Luitzen Brouwer o logica intuizionistica.

Questa è la prima alternativa che propongo alla logica classica. Proverò a spiegare la natura di questa alternativa.

Brouwer è un matematico olandese, ma è molto vicino alla filosofia e soprattutto alla filosofia della matematica. Egli sostiene, ad esempio, che il numero sia una costruzione mentale, ma la sua concezione del numero lo avvicina molto a quella di Kant, il quale affermava che il numero è una sintesi attiva a partire dalla forma a priori del tempo.

La logica intuizionistica, in ogni caso, certamente ha Brouwer come padre, ma la sua storia vanta molti altri nomi.

Arend Heyting ha sviluppato i sistemi formali per la logica intuizionista sia come logica enunciativa sia come logica predicativa. Inoltre Heyting è famoso anche per l'aritmetica intuizionistica.

Contributi alla logica intuizionistica li hanno dati anche filosofi analitici come Kurt Gödel o Saul Kripke.

Nella logica intuizionistica si rifiuta il principio di terzo escluso, in quanto completamente indimostrabile nel caso delle strutture infinite (si pensi a Cantor).

In effetti non è possibile verificare in quel caso se tutti gli oggetti hanno una data proprietà e tanto meno che vi sia un oggetto che non l'ha, perciò non posso dire che o esiste una x che ha tale proprietà o non esiste.

Inoltre nella logica intuizionistica se si ammette che asserire un certo stato di cose è falso non si dice che l'enunciato che predica l'assenza di quello stato di cose è vero, piuttosto la verità dipende dagli osservatori. Per questo per la logica intuizionistica la doppia negazione non è dimostrabile.

Come con la logica modale, anche nella logica intuizionistica vi sono due tipi di logica:

logica intuizionistica enunciativa;

logica intuizionistica predicativa.

Non parlerò di tutte e due i tipi di logica, perché sarebbe molto lungo, mi concentrerò solo sulla logica intuizionistica predicativa. I simboli di questa forma di logica sono grosso modo gli stessi della logica classica.

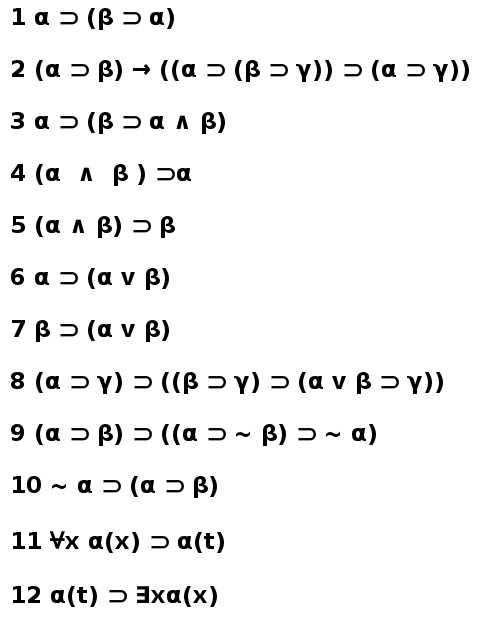
In realtà la logica intuizionistica non si può dire che cambi da quella classica per via dei simboli logici usati o per le espressioni, quanto piuttosto per i teoremi che si possono dimostrare e il modo stesso di pensare la logica che non è più assoluto, ma è relativo al soggetto che la usa e asserisce certi enunciati.

La logica intuizionistica certamente è un'alternativa alla logica classica, ma ve ne sono molte altre:

la logica paraconsistente; la logica quantistica; la logica lineare; la fuzzy logic e altro ancora.

La logica classica, quella che è nata ed è stata sviluppata con la filosofia è chiaramente oggi solo uno dei tanti tipi di logica. Data la grande varietà dei tipi di logica è importante che la filosofia si apra anch'essa a questa molteplicità di risorse.

Da questi fatti si possono pensare almeno due cose: o che la logica classica ha bisogno di essere implementata oppure che il suo campo di validità deve essere ristretto.

Di fatto la logica classica non riesce a cogliere una serie di fenomeni, spesso fenomeni che ricadono sotto la categoria di "processo", proprio perché parte da una visione ontologica molto precisa e abbastanza lacunosa.

I presupposti ontologici della logica classica sono bene espressi nello scritto di Wittgenstein: il famoso Tractatus logicus-philosophicus.

In quel testo Wittgenstein afferma che il mondo è la totalità dei fatti e che l'enunciato è un'immagine del mondo o un modello che esprime un fatto.

Se effettivamente esiste un fatto che corrisponde all'enunciato, allora l'enunciato è vero, se non è così, allora l'enunciato è falso.

Il mondo è davvero fatto solo di fatti? beh, come minimo potremmo chiederci come si sono costituiti questi fatti, non possiamo certo pensare che le cose così come sono ora, lo fossero da sempre.

Un po' come nella filosofia di Husserl si riconosce un aspetto strutturale e uno genetico, così si dovrebbe fare anche con il mondo, tuttavia Wittgenstein riconosce solo l'aspetto strutturale.

La mancanza dell'elemento genetico: l'obbiezione di Husserl a Frege.

Il continentale ha sempre obbiettato all'analitico che l'analitico misconosce la componente storica della realtà, pensando le cose come fossero eterne o enti del terzo regno del senso (versione moderna del mondo delle idee di Platone).

Secondo me uno dei problemi della logica è che la logica non ci permette di cogliere il divenire, ma il divenire delle cose è pur sempre una parte fondamentale della realtà.

Il divenire è stato condannato dalla filosofia antica, salvo Eraclito, proprio perché si pensava violasse le leggi della logica, in particolare la legge della non contraddizione.

Parmenide faceva questo ragionamento: il divenire non può essere, perché nel divenire si mescolano essere e non essere.

Dal punto di vista logico sarebbe come dire: ~Ed ∧ Ed, dove si predica al divenire (d) due proprietà opposte come l'essere (E) e il non essere (~E).

Zenone diceva che l'uomo non muore perché o muore da vivo o muore da morto, ma se muore da vivo vive e muore allo stesso tempo, mentre se muore da morto, allora è già morto, perciò è impossibile che egli muoia.

Secondo me si giudica il divenire come contraddittorio perché lo si pensa di nuovo riconducendolo a dei fatti.

Seguite questo esempio: un oggetto rosso diviene non rosso; perché l'oggetto rosso diventi non rosso bisogna che vi sia un momento intermedio in cui l'oggetto sia sia rosso che non rosso, ma questo è contraddittorio; dunque il divenire è contraddittorio.

Quello che accade in questo ragionamento è che si parte da uno stato di cose e si passa ad un altro stato di cose. Il divenire è concepito come il passaggio stesso tra i due stati di cose.

Questo passaggio sembra presupporre un momento intermedio, un momento impensabile perché genera una contraddizione, ma se non lo si pensasse il divenire non sarebbe affatto possibile.

Il divenire può essere un fatto se si intende che un certo ente è mutato, ma questo non ci dice nulla sul processo del mutamento.

A mio avviso per comprendere il divenire bisogna rifarsi ad un altro modello di logica: la logica del senso.

Logica del senso è un libro scritto dal filosofo Gilles Deleuze.

In questo libro da un lato il filosofo costruisce una logica del senso, dall'altro dimostra che il divenire non è affatto contraddittorio.

Logica del senso non è più una logica formale come quelle precedenti, ma è una logica basata su paradossi. Il modello di Deleuze è quello dello strutturalismo.

Secondo lo strutturalismo il linguaggio è un sistema di segni e il segno è un algoritmo che segue la formula: significato/significante. Il senso nell'algoritmo è il significante.

Nella formula troviamo due serie: quella del significato e quella del significante. Gli elementi di queste due serie sono singolarità, punti che rimandano da una serie all'altra ad un altro punto per lo stesso grado o tipo.

Le due serie sono divise da una barra, ma la serie del significante eccede su quella del significato. Si potrebbe pensare la serie significante come parole e la serie del significato come cose. L'unica componente del linguaggio che fa si che le parole non si riducano alle cose è il verbo. Il verbo è l'eccedenza di significante sul significato. Il verbo è puro evento. Se il significante eccede sul significato, vuol dire che c'è un'eccedenza di senso e un'assenza di significato. Un esempio sono quelle parole-baule di Carroll, spesso citate da Deleuze, come: Jabberwocky (Ciciarampa). La parola baule non vuol dir niente, ma ha comunque un senso.

Nella logica del senso è il non-senso, quindi la mancanza di significato, come casella vuota, che fa funzionare al contrario tutta la struttura. Come nello specchio di Carroll: tutto è al contrario, prima sento male e poi mi ferisco.

La logica del senso segue principalmente tre paradossi:

1) Paradosso della regressione: nello strutturalismo questo paradosso è espresso in questo modo: il significato di un significante è un altro significante.

Questo significa che se io voglio comprendere il senso di un'enunciato devo formulare un altro enunciato che avrà un altro senso, ma ovviamente questo implica che devo formulare un altro enunciato con ancora un altro senso, se voglio capire il senso del secondo enunciato.

Questo paradosso ha la forma del regresso: n1 → n2 → n3 → n4... Molti di questi paradossi di Deleuze sono ispirati ai romanzi di Caroll, qui Deleuze ha in mente il paradosso del nome della canzone. Il cavaliere parla con Alice e gli dice che il nome della canzone è Occhi di merzullo, poi gli dice che il nome vero è Il vecchio, vecchio uomo, poi il cavaliere ci dice che la canzone viene chiamata Vie e mezzi, ma è solo un modo in cui viene chiamata perché, dice il cavaliere, la canzone è Seduti su un cancello. È facile vedere il regresso dei nomi: (Occhi di merluzzo) 1 → (Il vecchio, vecchio uomo) 2 → (Vie e mezzi) 3 → (Seduti su un cancello) 4...

2) Paradosso dello sdoppiamento sterile: se vogliamo evitare la regressione nel senso, possiamo tentare di immobilizzare il senso ed estrarne la pellicola dall'enunciato, ma tutto quello che otterremo sarà un espressione sterile.

"Il cielo è azzurro" diventa "il cielo azzurreggiante", "Dio esiste" diventa "Dio esistente". Questo paradosso in Carroll è il paradosso del sorriso senza gatto. Nella scena famosa Alice vede il sorriso del gatto di Cheshire senza il suo corpo. Questo fenomeno manifesta il senso puro che è puro evento e non uno stato di cose. Nel sorriso senza gatto l'evento si dà senza il corpo, la proprietà senza la sostanza.

3) Paradosso della neutralità: il senso ha una caratteristica speciale: è indifferente ad ogni opposizione ed è sempre doppio (attivo-passivo, passato-futuro).

Deleuze collega anche la logica del senso alla teoria degli insiemi nella versione di Russell.

Deleuze spiega il paradosso di Russell del barbiere attraverso l'esistenza di un insieme anomalo, un insieme che contiene elementi di tipo diverso. Inoltre usa la nozione di "tipo" della teoria del tipi per spiegare il problema del "grado" nel regresso del primo paradosso.

Sul piano del significato Deleuze sembra concordare con Russell, ossia afferma che il significato fissa i valori di verità dell'enunciato (1,0), se all'enunciato corrisponde uno stato di cose espresso dall'enunciato stesso allora l'enunciato è vero (1), altrimenti è falso (0). Il senso non è né vero e nemmeno falso, ma presiede alla genesi della verità in quanto creazione.

Il piano del senso è quello del problema. Per capire in che senso davvero questa logica di Deleuze offre una visione diversa del divenire, visione nella quale il divenire non più contraddittorio, bisogna ripartire dal terzo paradosso.

Il terzo paradosso tocca un punto cruciale: il senso segue la logica della disgiunzione inclusiva. Nella logica la tavola della verità della disgiunzione è la seguente:

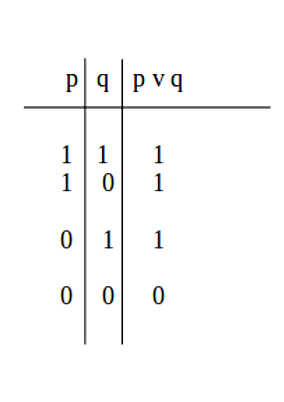
Il problema riguarda la prima riga: c'è chi pensa che la disgiunzione inclusiva sia semplicemente il caso in cui in una disgiunzione entrambi i disgiunti risultano veri (1,1).

Questa definizione è discutibile: è discutibile se possa essere vero l'enunciato "questa maglia o è verde o è rossa", quando la maglia è sia verde che rossa. Oltretutto non si potrebbe dire che questo si valido nel caso dell'enunciato "p v ~ p", altrimenti si otterrebbe una contraddizione.

Per disgiunzione inclusiva in logica del senso si intende un caso dove si assiste ad un fenomeno di doppia affermazione, un caso doppia direzionalità. Il divenire secondo Deleuze segue proprio questa logica.

Deleuze legge il divenire a partire dalla nozione degli stoici di Aiôn. Nell'Aiôn il tempo si divide sempre in passato e futuro simultaneamente, ogni evento è sempre già stato e nello stesso tempo deve ancora avvenire.

Ancora una volta Alice è l'esempio: Alice non è "più grande" e "più piccola" allo stesso tempo, ma è nello stesso tempo che lo diviene.

Il tentativo di Deleuze consiste nel pensare una forma di tempo non metrico. Nella geometria si parla di spazio metrico nel caso di un insieme di punti con delle distanze fissate. Normalmente lo spazio metrico è associato alla geometria euclidea.

Lo spazio non metrico, invece, è tipico delle geometrie non euclidee (es. geometria differenziale). Deleuze usa molto queste nozioni di spazio, ma usa anlogalmente nozioni simili nel tempo.

Il tempo metrico è il Kronos, un tempo come successione di presenti, presenti che unificano il passato e il futuro. Il tempo non metrico è l'Aiôn. In ambito scientifico non esiste una forma di tempo equivalente, probabilmente deve essere ancora scoperta e questo spiega anche quanto poco gli scienziati si interessino del divenire.

Secondo me il terzo paradosso della logica del senso spiega perché il divenire non è contraddittorio. Il divenire non è un passaggio da uno stato di cose ad un altro, è piuttosto un processo virtuale neutro rispetto agli opposti che ha due attualizzazioni differenti in due momenti del tempo distinti.

L'attualizzazione consiste in una metrizzazione di un tempo non metrico. Un esempio: supponiamo che una sfera blu diventi rossa; il divenire non consiste nella sfera blu che poi con una serie di passaggi intermedi diventa rossa, ma in un processo virtuale neutro rispetto al rosso e al blu, il quale ha due attualizzazioni diverse, in due momenti diversi, una nella sfera blu e l'altro nella sfera rossa.

In questo modo non c'è nessuna contraddizione, l'unico problema che può sorgere riguarda il principio di terzo escluso. Bisogna vedere in base a come si concepisce la disgiunzione inclusiva se questa viola tale principio o meno.

Si noti ancora una cosa: Wittgenstein coglie acutamente che la dimensione della logica è il presente. Se è vero l'enunciato "Socrate corre" è perché attualmente Socrate sta correndo. Il tempo presente si colloca in ciò che Deleuze chiama Kronos.

Per Deleuze la logica classica riguarda il mondo attuale, ma fallisce di comprendere il virtuale. Si potrebbe addirittura dire con Bergson che il presente è illusione e che ogni volta che diciamo "presente" è già passato.

Questo fatto non gioca a favore della logica.

Un altro filosofo che ha certamente affermato l'esigenza di pensare più modelli logici oltre a quello classico e che ha mostrato i limiti della logica classica è certamente Gilbert Simondon.

Simondon è famoso per la sua nozione di individuazione. Simondon si è interessato, come anche Deleuze del resto, del processo di formazione dell'individuo. Notoriamente l'individuo era l'elemento escluso nella Metafisica di Aristotele. A

ristotele affermava che dell'individuo non c'è scienza, perché la scienza è solo del generale. Qual'è il problema con l'individuo? L'individuo è unico, del tutto irripetibile.

È davvero difficile parlare dell'individuo, posso dire che una cosa è gialla e pensare con questo di dire qualcosa di informativo sull'individuo perché tutti gli altri individui sono verdi, ma ogni volta predico delle qualità generali e non sto parlando di quel giallo lì, quello unico, che non si può dire. Aristotele spiega l'individuo come unione di materia e di forma.

L'unione è possibile, secondo Aristotele, grazie alla causa efficiente. Platone parte anche lui dalla materia e dalla forma, ma spiega l'unione a partire dalla metexis, ossia la partecipazione della materia ad un certo grado nell'idea.

Non è mai stato chiaro bene come funzionasse il processo di formazione dell'individuo. Spesso si partiva dall'individuo come già dato, senza pensarlo come un prodotto di un processo. Altre volte si diceva che l'individuo dipende da un principio: il principio individuazionis.

Con Simondon avviene qualcosa di straordinario: Simondon ci fornisce una teoria sulla formazione dell'individuo a partire dalla sua nozione di individuazione, sfruttando il concetto di energia potenziale della fisica.

Prima di spiegare i dettagli di tutto questo processo è importante dire due cose: secondo Simondon per l'individuazione non vale il principio della logica del terzo escluso; secondo Simondon siccome sono molti i modi dell'individuazione, devono essere molti i modelli di logica. Non si può accattare il terzo escluso perché prima della costituzione dell'individuo non si può dire che sia questo o quello, solo una volta che esso si è costituito, si può dire che l'individuo come prodotto ha quella caratteristica piuttosto che la sua opposta. Sulla necessità di una pluralità di logiche si legga il seguente passaggio:

«Se è vero, come è vero, che la logica si orienta su enunciati relativi all'essere solo dopo l'individuazione, occorre istituire una teoria dell'essere precedente ad ogni logica: tale teoria può servire da fondamento alla logica, poiché nulla prova, prima d'ogni altra cosa, che l'essere sia individuato in un solo modo possibile. Se esistono infatti diversi tipi di individuazione, dovrebbero sussistere altresì diverse logiche, ognuna di esse riferita ad un particolare tipo di individuazione. La classificazione delle ontogenesi permetterebbe di pluralizzare la logica con valido fondamento di pluralità.» (Simondon, Gilbert, L'individuazione alla luce delle nozioni di forma e d'informazione, Mimesis, Milano, 2011)

Simondon spiega l'individuazione in vari campi del sapere: chimica, fisica quantistica, biologia, tecnica, psicologia. Tuttavia si può cercare di estrapolare una visione generale sull'individuazione in Simondon. Innanzitutto occorre precisare che il concetto di individuo qui viene applicato a tantissime cose, cose a cui forse, l'uomo comune non lo applicherebbe.

Individui siamo noi, gli animali, le cellule, i cristalli, le particelle, un mattone, ma anche un branco di lupi o una folla di manifestanti (non i singoli manifestanti, ma la folla stessa è un individuo). Simondon infatti introduce anche la nozione di individuazione di gruppo con la famosa nozione di "transindividuale".

Perché si possa parlare di genesi dell'individuo bisogna prima di tutto pensare il pre-individuale, ossia una dimensione che preceda l'individuo. Il pre-individuale è un essere senza fasi, pura energia potenziale non attualizzata in una condizione di metastabilità, ossia ben lontana dalle condizioni dell'equilibrio. Il processo di generazione dell'individuo consiste nell'attualizzazione dei potenziali nella strutturazione.

Simondon spiega che l'energia potenziale è quell'energia attraverso la quale si possono attuare delle trasformazioni in un determinato sistema. Tuttavia Simondon spiega che perché vi sia energia potenziale in un sistema vi deve essere disimmetria. Quando due pendoli non sono sincronici, allora si dà uno scambio di energia nel sistema.

Un altro caso è quello del corpo che ha una data temperatura, ma ha una parte più calda e una più fredda. Molti di questi riferimenti sull'energia potenziale vengono dalla termo dinamica e solo in parte si riferiscono ad Einstein. Esempi di individuazione di Simondon sono il mattone, il cristallo e la particella. La cosa interessante della teoria è il riconoscimento dell'aspetto processuale nella formazione dell'individuo, un elemento difficile da catturare e da esprimere con la logica classica.