L'ontologia con la teoria degli insiemi: Alain Badiou e il teorema di Cantor

Alain Badiou ha scritto diversi testi sul tema della matematica: Il concetto di modello, L'essere e l'evento, Il numero e i numeri, Le logiche dei mondi.
Il concetto di modello è un testo di epistemologia della matematica, in particolare tratta i temi della logica predicativa e del concetto di modello nella logica predicativa.
L'essere e l'evento è il testo più famoso di Badiou, in questo testo Badiou costruisce un'ontologia basata sulla teoria degli insiemi.
Il numero e i numeri è un testo di filosofia della matematica che ha il compito ambizioso di fondare la nozione di numero sull'ordinale cantoriano.
Le logiche dei mondi è un testo che tratta i temi della fenomenologia e del trascendentale in chiave logica.
Non ho intenzione di parlare di tutte queste opere, quello che dirò può essere attribuito soprattutto a L'essere e l'evento.
Prima di parlare effettivamente di come Badiou usa Cantor per pensare una nuova ontologia su basi matematiche, cercherò di scrivere almeno sulle nozioni più basilari della teoria degli insiemi, di modo che dopo sia più comprensibile quel che dirò su Cantor e il teorema di Cantor.
Prima di tutto bisogna saper riconoscere il linguaggio della teoria degli insiemi e saper leggere i suoi simboli.

Ogni insieme ha come sotto insieme un insieme vuoto, anche l'insieme vuoto. Un insieme con n elementi è un insieme finito.
Supponendo che l'insieme sia di studenti e che n = 3, allora: A = {Alberto, Giuseppina, Noemi}. Tra parentesi graffe si mettono tutti gli elementi dell'insieme.
Un esempio di insieme infinito è l'insieme dei numeri naturali (ℕ): {1, 2, 3, 4, 5, 6, 7, 8, ecc.}. Un insieme (A) è sottoinsieme di un altro insieme (B), il quale (B) è soprainsieme del primo (A), quando gli elementi del primo (A) insieme sono tutti elementi del secondo (B).

All'interno dell'insieme va distinto l'insieme con i suoi elementi dall'insieme delle parti dell'insieme stesso.
Questo è molto importante e serve a Badiou per dimostrare, in un certo senso, che quel che si afferma in filosofia, quando si dice che "il Tutto è maggiore delle parti", in realtà risulta falso. All'interno della teoria degli insiemi, l'insieme delle parti è sempre eccedente l'insieme totale.

A destra stanno gli insiemi con i loro elementi (A, B, C), a sinistra stanno gli insiemi delle loro parti (P(A), P(B), P(C)).
L'insieme delle parti comprende tutti i sotto insiemi dell'insieme totale, quindi prima di tutto l'insieme vuoto, poi gli insiemi che contengono gli elementi singoli, poi gli insiemi delle loro combinazioni, ossia si raggruppano tutti gli elementi per ogni combinazione.

Date le definizioni che scritto fino ad ora, si possono ricavare le seguenti espressioni:

Prima di parlare di relazioni e funzioni negli insiemi, vorrei ancora citare alcune definizioni: differenza negli insiemi; differenza simmetrica; prodotto degli insiemi. Non parlerò di diagrammi di Venn o cose simili, non è il caso, non ho gli strumenti grafici per farlo e non credo che servirà.
La differenza negli insiemi si definisce in questo modo: dati due insiemi A e C, la differenza tra i due insiemi (A/C) è l'insieme degli elementi di A che non sono di C.
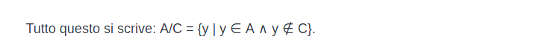
La differenza simmetrica si definisce in questo modo:

Le relazioni hanno varie tipologie:
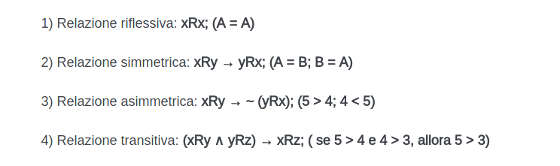
Veniamo ora alle funzioni. Una funzione (F) associa per ogni elemento di un insieme un elemento del secondo.
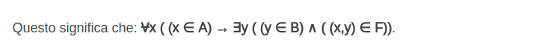
Il primo insieme è il dominio ed è il dominio della funzione, il secondo è il codominio. Una funzione è di A su B, se A è il dominio e B il codominio.
La funzione segue questa formula: F (x) = y, dove (x) è l'argomento e y il valore della funzione.
Un esempio: M (2,2) = 4, supponendo che M = moltiplicazione, dunque 2 x 2 = 4.
La funzione mi permette di, dato un elemento di un insieme, associare un elemento di un altro insieme o anche più di uno. Faccio un esempio preso dai database o tipico di certi sistemi che si usano nella Business Intelligence.
Prendiamo due insiemi: A = studenti; B = corsi di studio. L'insieme A contiene cinque elementi: {Alberto, Giuseppina, Noemi, Claudio, Fabio}.
L'insieme B contiene anch'esso cinque elementi: {storia contemporanea, web of things, storia greca, programmazione Java, storia della letteratura spagnola}. Per dire che Noemi segue il corso di storia greca, e collegare quindi due data base, posso usare anche delle funzioni, una volta che penso i data base come degli insiemi. Posso scrivere F (Noemi) = storia greca. Le funzioni possono essere di vario tipo:
1) Funzione suriettiva: si parla di funzione suriettiva quando ad un elemento del dominio può essere legato uno o più elementi del codominio. Esempio: Noemi segue i corsi di storia greca e storia contemporanea.
2) Funzione iniettiva: si parla di funzione iniettiva quando ad elemento del dominio si può collegare uno e uno solo del codominio.

Esempio: Fabio segue solo il corso di web of things.
3) Funzione biunivoca: si parla di funzione biunivoca se ad un elemento del dominio corrisponde un solo elemento del codominio e viceversa. Esempio: Claudio è l'unico che segue il corso di storia della letteratura spagnola.
Questi concetti sono essenziali per capire il teorema di Cantor.
Ora è venuto il momento entrare di più nella filosofia di Badiou.
Badiou pensa che l'ontologia riguardi i corpi, ma i corpi non sono che dei molteplici, questo molteplici vengono letti da parte di Badiou attraverso gli ordinali di Cantor.
Penso che questo problema vada collegato al vecchio problema in filosofia dell'Uno e dei Molti.
Se prendo una zolletta di zucchero, la zolletta sarà compatta, dolce e ha la forma di un cubo. L'insieme delle proprietà è sufficiente a formare una zolletta di zucchero? la zolletta di zucchero unificando le proprietà è forse più delle sue singole parti?
Questi sono esempi di problemi che hanno a che fare con il problema dell'Uno e dei Molti, tratti dal mondo di tutti i giorni. Dire che il corpo è molteplicità è chiaramente da intendere nel senso delle sue parti, ma le parti, come ho mostrato con gli insiemi, sono molte.
Il numero ordinale concerne l'ordine degli elementi nell'insieme. Numeri ordinali: primo, secondo, terzo, ecc.
Per un buon ordine degli ordinali secondo Cantor sono richiesti due presupposti:

Dunque ogni elemento o è uguale ad un altro, o è maggiore o è minore. Inoltre c'è sempre un elemento più piccolo, rispetto al quale tutti gli altri elementi sono maggiori.
In questo modo posso ordinare gli elementi nell'insieme: sia l'elemento più piccolo l'elemento 1, allora, chiamando l'insieme E: E - 1 = 2. Oppure E - (1, 2) = 3, ecc. In questo modo ordino i termini (1, 2, 3, 4, ecc.).

Attraverso l'ordinale metto in ordine gli elementi di un insieme, ma se voglio conoscere la grandezza di un insieme devo usare un altro numero: il numero cardinale.
Se prendo un insieme qualsiasi, ad esempio A = {Alberto, Giuseppina, Noemi, Claudio, Fabio}, attraverso una corrispondenza biunivoca (con funzione iniettiva) tra gli elementi di questo insieme e quelli dell'insieme {0,...,n-1}, posso comprendere la cardinalità del primo insieme.
Questo metodo è stato inventato da von Neumann.

Assegnando ad ogni elemento del primo insieme un elemento del secondo (es. F(Alberto) = 0) avremo una corrispondenza biunivoca tra i due insiemi e perciò possiamo trattare in maniera rigorosa la cardinalità.
In questo caso la cardinalità è uguale a cinque (│A│= 5). Questo procedimento è molto facile quando l'insieme è finito, ma che fare quando gli elementi sono ω, quindi sono infiniti?
È che qui che viene il bello, qui è Cantor che ha la soluzione: il cardinale transfinito.

Un esempio: si prenda l'insieme dei numeri pari e l'insieme dei numeri naturali.
Se vogliamo trovare una corrispondenza biunivoca dovremo fare in questo modo: F(1) = 2, F(2) = 4, F(3) = 6, F(4) = 8, ecc.
Per ogni numero naturale si assegna un numero pari seguendo l'ordine e andando all'infinito.

I cardinali transfiniti sono infiniti, non esiste un cardinale transfinito più grande. Questo fatto è di estrema importanza per la filosofia.
Cantor ha in pratica ha dimostrato che gli infiniti sono infiniti e non è che ce ne sia uno solo. Cantor ha inoltre dimostrato che l'infinito non implica contraddizioni, ma che è possibile trattare rigorosamente gli infiniti secondo ordini di grandezza.
Questo fatto dovrebbe essere già cruciale per capire cosa vuole dimostrare il teorema di Cantor, ossia che non esiste il Tutto, che alla fine non c'è un insieme di tutti gli insiemi.
Badiou fa tesoro di tutte queste scoperte e le applica in ontologia.
Se due insiemi (A, B) sono in corrispondenza biunivoca, allora hanno la stessa cardinalità (│A│=│B│). Quando due insiemi hanno la stessa cardinalità si dice che sono equipotenti.
Badiou distingue lo stato dalla situazione. Mentre la situazione presenta degli uni molteplici, lo stato ripresenta le parti di questi molteplici.
Il teorema di Cantor afferma che il cardinale dell'insieme delle parti è maggiore di quello dell'insieme iniziale.
Il teorema di Cantor è dimostrato da Badiou in questo modo:
Ipotizziamo per assurdo che vi sia una corrispondenza biunivoca f tra l'insieme A e l'insieme delle sue parti p(A).
Una corrispondenza biunivoca si ha quando esiste una funzione che assegna per ogni elemento di un dominio (A) uno e uno solo elemento del codominio (p (A)).
Ipotizziamo l'esistenza di un elemento y in A, allora in p(A) vi sarà un elemento corrispondente come valore della funzione f(y). Dire che c'è corrispondenza biunivoca tra i due insiemi significa che:│A│=│p(A)│.
Se c'è corrispondenza biunivoca si dice che gli insiemi sono equipotenti. Ogni elemento y di A corrisponde ad una parte di A, che è un elemento di p(A). Per ogni elemento y di A esiste un elemento f(y) che gli corrisponderà in p(A).

Nell'insieme A esiste una parte che corrisponde all'insieme di tutti gli elementi f-esterni, questa parte, siccome esiste una corrispondenza biunivoca tra A e p(A), deve corrispondere per f ad un elemento x, tale per cui f(x) = l'insieme di tutti gli elementi f-esterni di A.
Bisogna dimostrare che x non può essere f-interno e nemmeno f-esterno.

Prima contraddizione.

Seconda contraddizione.
Il teorema dimostra che A e p(A) non sono equipotenti, cioè che │A│<│p(A)│, dunque la cardinalità non è la stessa.
Il teorema di Cantor dimostra che l'insieme dei numeri naturali N non è equipotente con l'insieme delle sue parti P(N), infatti P(N) > N.
Questo teorema porta alla conclusione che non può esistere un insieme degli insiemi, infatti se esistesse, possiamo che si chiami W, allora P(W) > W.
In filosofia questo, dal punto di vista ontologico nega ogni tipo di entità che pretende di comprendere ogni cosa.
Kant ha definito il mondo come totalità dei fenomeni esterni, Badiou deriva dal teorema di Cantor e il paradosso di Russell che il mondo non esiste.
Secondo Badiou dire che il mondo non c'è vuol dire che non c'è la totalità, ma, al contrario, ci sono infiniti mondi.
Badiou ha individuato almeno cinque tipologie di mondi: mondo interno; mondo storico; mondo sociale; cosmo; mondo biologico.
In Le logiche dei mondi Badiou sviluppa molto meglio questa teoria con la logica. Quest'ultimo libro è la continuazione di L'essere e l'evento. Non parlerò di questa continuazione e quello che ho detto, in realtà è solo un piccolissimo assaggio di L'essere e l'evento.
Badiou crede che l'esistenza non sia altro che l'apparire in un mondo, ma di mondi ce ne sono infiniti. Morire, a questo punto, vuol dire cessare di apparire in un mondo.
La vera rivoluzione è questa: il nostro mondo non ha più nulla di centrale, è soltanto uno dei tantissimi mondi.
Oggi se ci chiediamo se qualcosa esiste, dovremmo prima chiederci a quale mondo ci riferiamo, prima di dare una risposta.
L'esistenza è relativa al dominio. Esempi: Harry Potter esiste solo nei romanzi o nei film; i pianeti esistono relativamente al cosmo; Napoleone esiste relativamente al mondo della storia e a certi altri domini.
Quel che ha fatto Badiou è molto importante perché ha iniziato a pensare l'ontologia in termini matematici. Questo passo è essenziale per andare sempre più nella direzione di una filosofia come scienza fondata sulla matematica.
Per questo penso sia essenziale il pensiero di Badiou, perché ha porto di molto avanti la sperimentazione matematica in filosofia e soprattutto lo ha fatto nella tradizione continentale che era ancora piuttosto lontana da un metodo matematico.
